Microarquitectura
es un proyecto realizado por Sara San Gregorio en relación con
Medialab-Prado en Madrid.
Las siguientes imágenes son ejemplos de actividades realizadas en Medialab-Prado con Microarquitectura:
Así nos describe Sara San Gregorio este trabajo:
"Microarquitectura es un juego de autocostrucción de cabañas para niñas y niños compuesto en un kit de piezas planas para experimentar el volumen,
el espacio, la construcción y el juego. Es un proyecto desarrollado en Medialab-Prado durante la convocatoria abierta a realizar proyectos
haciendo uso de su laboratorio de fabricación digital en 2015 .Todo el proceso de ideación y diseño así como sus archivos de fabricación
están publicados en el blog microarquitectura.org bajo la licencia CC-BY-NC-SA. La investigación previa para determinar la forma de las
piezas parte del estudio geométrico de diferentes poliedros y la alteración de la geometría plana que los componen para crear volúmenes que
dibujen los espacios de juego dándo tanta importancia a la forma del hueco como a la forma de las caras de madera
incorporando en este desarrollo geométrico variables como la optimización del material y el uso de las máquinas de fabricación digital."
En esta página vamos a explorar algunas posibilidades de Microarquitectura en relación con la construcción de poliedros, estructuras
en las que la simetría juega un papel fundamental.
Estas son las dos formas básicas de Microarquitectura.
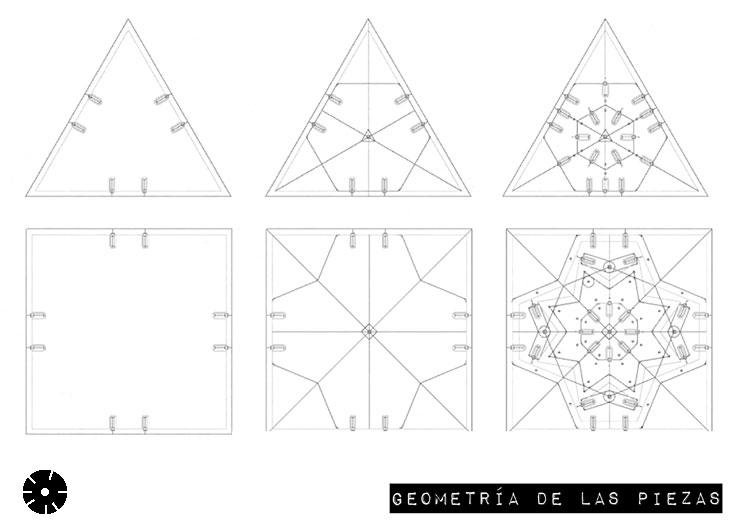
Una es un hexágono regular que podemos ver también como un "triángulo equilátero truncado". La otra se basa en el cuadrado y el octógono,
pero no se trata de un
octógono regular. La podemos ver como un "cuadrado truncado".
Estas formas y las uniones pueden hacerse en diferentes tamaños y materiales: madera, metacrilato, cartón ...
Combinando tetraedros truncados y tetraedros se tesela el espacio. Podríamos ir añadiendo todas las piezas que quisieramos formando la estructura.
INVESTIGA
El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.
El tetraedro truncado es un sólido arquimediano que tiene 4 triángulos y 4 hexágonos.
El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su tetraedro truncado.
El octaedro truncado tiene una propiedad muy interesante que es que tesela el espacio. Es decir, con diferentes copias de este poliedro
rellenamos el espacio sin dejar huecos.
Con Microarquitectura se puede hacer esta preciosa construcción pero se necesita que los hexágonos tengan ranuras para poner uniones
en todas las aristas. El resultado será muy bonito. Aquí reproducimos esta idea con cartulina y gomas.
INVESTIGA
El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.
El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro.
Las caras octogonales de este cubo truncado construido con Microarquitectura no son regulares. Este poliedro es una ligera deformación del
correspondiente poliedro arquimediano (cuyas caras son octógonos regulares).
INVESTIGA
Truncando un cubo podemos obtener un cubo truncado y un cuboctaedro. Si truncamos un octaedro podemos conseguir un octaedro truncado y, también, un cuboctaedro.
La siguiente construcción se basa en el cuboctaedro, que es un sólido arquimediano formado por seis cuadrados y
ocho triángulos.
Si cortamos los vértices obtenemos un cuboctaedro truncado. Realmente lo que conseguimos no es un sólido arquimediano pues los
cuadrados resultan ser rectángulos. Deformando estos rectángulos en cuadrados obtenemos el sólido arquimediano que conocemos por
cuboctaedro truncado (formado por octógonos, hexágonos y cuadrados).
Al construir esta figura con Microarquitectura ocurre algo parecido. Los octógonos no son regulares y los cuadrados resultan ser rectángulos.
Es interesante notar que estos rectángulos tienen la misma forma (son semejantes) que los rectángulos de papel que llamamos folios y
que tienen un interesante formato estandarizado llamado DIN A (DIN A4 sería el folio).
Aprovechando la flexibilidad del material se puede construir esta figura también inspirada en el cuboctaedro truncado.
INVESTIGA
El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.
El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.
El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.
La estructura de una cabaña muy bonita es un rombicuboctaedro al que se han truncado los vértices.
INVESTIGA
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su rombicuboctaedro.
El icosidodecaedro es un sólido arquimediano formado por pentágonos y triángulos.
Truncando los vértices obtenemos el icosidodecaedro truncado que es el sólido arquimediano "más grande" que se construye usando polígonos
con la misma arista.
REFERENCIAS
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
MÁS ENLACES
Exposición sobre los cinco sólidos platónicos: tetraedro, cubo, octaedro, icosaedro y dodecaedro. Construcción de los poliedros encajados. El Omnipoliedro. Algunas propiedades básicas que se pueden aprender de esta construcción.
Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.
Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.
Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.
Material para la sesión del TTM (Zaragoza, el 10 de marzo de 2023). Con plantillas para descargar y construir varias figuras geométricas.
Material para la sesión del TTM (Zaragoza, el 20 de Octubre de 2017). El objetivo principal es disfrutar con las Matemáticas y fomentar la construcción de poliedros por su valor estético y también porque nos facilitan la comprensión de resultados matemáticos.
Material para la sesión del TTM (Zaragoza, el 19 de Octubre de 2018). Diferentes construcciones del icosaedro nos ayudan a comprender sus propiedades. El objetivo principal es disfrutan construyendo poliedros.
Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.
Podemos dibujar los desarrollos planos en cartulina y construir poliedros uniendo solapas con pegamento.
Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.
Técnica simple para construir poliedros pegando discos de cartulina.
El diseñador italiano Bruno Munari pensó 'Acona Biconbi' como un trabajo de escultura. También es un juego de construcción con el que podemos jugar con colores y formas.
Tubos de plástico o aluminio unidos son muy útiles para construir esqueletos de poliedros.
Con tres rectángulos áureos podemos construir un icosaedro.
Un icosaedro se puede poner dentro de un octaedro de modo que sus 12 vértices estén en las 12 aristas del octaedro. Dos construcciones nos ayudan a comprender esta relación y, gracias a ella, calcularemos el volumen del icosaedro.
El origami modular es una técnica preciosa que consiste en plegar varias unidades independientes que se unen sin pegamento para formar poliedros.
Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.
Zome es un conjunto de piezas de plástico ideal para construir poliedros desmontables. De las infinitas posibilidades de Zome, aquí lo usamos para calcular el volumen del dodecaedro.
Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.
Construcción de un pequeño dodecaedro estrellado como metáfora del confinamiento que estamos viviendo por la pandemia del coronavirus COVID-19.
El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.
El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
El tetraedro truncado es un sólido arquimediano que tiene 4 triángulos y 4 hexágonos.
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su tetraedro truncado.
El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.
Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.
El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.
El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.
Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.
El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.
El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.
El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.
Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su rombicuboctaedro.
SIGUIENTE
ANTERIOR
