Tetraedro truncado (adaptado de Leonardo da Vinci)
Este vídeo se basa en una aplicación interactiva. Es una adaptación del dibujo que Leonardo da Vinci hizo del tetraedro truncado (tetracedron abscisus vacuus) para el libro 'La divina proporción' de Luca Pacioli.
Pacioli describe así el tetraedro truncado:
"El tetraedro despuntado o absciso sólido plano o hueco está contenido por dieciocho líneas que forman treinta y seis ángulos
superficiales y doce sólidos; por tanto, lo circundan ocho bases, cuatro de las cuales son hexagonales, es decir, de seis lados iguales,
y cuatro triangulares, es decir, de tres lados, igualmente equiláteras y equiángulas. Pero, de estas dieciocho líneas, doce son comunes
a las bases triagulares y hexagonales; y éstas son todas propias de los hexágonos, porque necesariamente los cuatro hexágonos juntos
forman con algunos de sus lados los cuatro triángulos, como la experiencia de su propia forma material nos muestra de modo evidente. Y
deriva del precedente -el tetraedro- mediante el corte uniforme de sus lados en tres partes iguales."
('La divina proporción' de Luca Pacioli, página, 90, traducción de Juan Calatrava, Editorial Akal, 4ª edición, 2008)
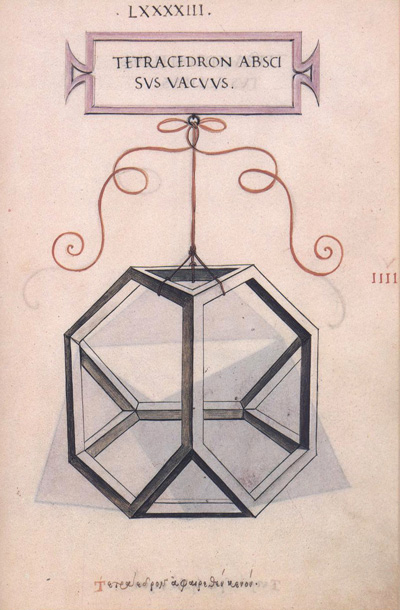
Dibujo de Leonardo da Vinci del tetraedro truncado (tetracedron abscisus vacuus) para el libro 'La divina proporción' de Luca Pacioli. (Hay versión española del libro 'La divina proporción' en Editorial Akal. La imagen se usa con permiso de la Editorial Akal).
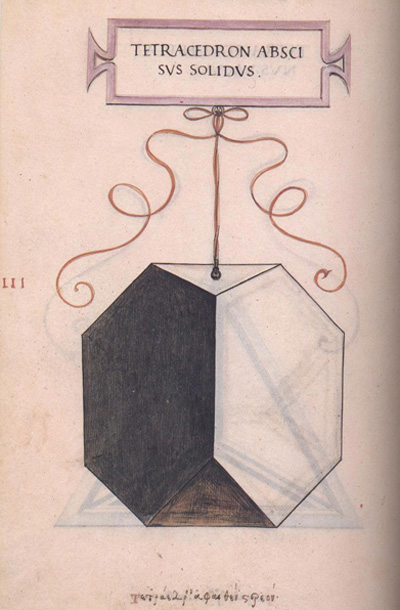
Dibujo de Leonardo da Vinci del tetraedro truncado (tetracedron abscisus solidus) para el libro 'La divina proporción' de Luca Pacioli. (Hay versión española del libro 'La divina proporción' en Editorial Akal. La imagen se usa con permiso de la Editorial Akal).
Jugando con la aplicación interactiva de esta página podemos obtener imágenes como éstas:



REFERENCIAS
Luca Pacioli - La divina proporción - Ediciones Akal, 4ª edición, 2004. Traducción de Juan Calatrava.
Leonardo da Vinci's Geometric Sketches artículo de Frank J. Swetz en MathDl, Loci:Convergence.
Leonardo da Vinci's Polyhedra página de George Hart en su excelente sitio sobre poliedros.
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro truncado.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su cuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su rombicuboctaedro.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación del poliedro de 72 caras (Septuaginta) también conocido como esfera de Campanus de Novara.

El octaedro estrellado fue dibujado por Leonardo para el libro 'La divina proporción' de Luca Pacioli. Años más tarde, Kepler nombró este poliedro stella octangula.

El poliedro compuesto por un cubo y un octaedro es un cuboctaedro estrellado. O lo que es lo mismo, el cuboctaedro es el sólido común al cubo y al octaedro en este poliedro.

Con medios cubos podemos formar el octaedro truncado. El cubo tesela el espacio y también el octaedro truncado. También calculamos su volumen.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.

El octaedro truncado es un sólido arquimediano que se puede obtener a partir de un octaedro truncando sus vértices. Su volumen se puede calcular a partir del volumen del octaedro.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices.

El cuboctaedro es un sólido arquimediano que se puede obtener a partir de un cubo truncando sus vértices. También se obtiene a partir de un octaedro truncando sus vértices

El octaedro truncado es un poliedro que tiene la propiedad de teselar el espacio: con poliedros congruentes podemos rellenar el espacio sin dejar huecos.
Truncando un cubo podemos obtener un cubo truncado y un cuboctaedro. Si truncamos un octaedro podemos conseguir un octaedro truncado y, también, un cuboctaedro.