Sólidos platónicos
Hay cinco poliedros que destacan por su regularidad (o simetría), son los llamados poliedros o sólidos platónicos.
El nombre de 'sólidos platónicos' proviene de que son nombrados por el filósofo griego Platón en su libro "Timeo"
(escrito en torno al año 360 a.C.),
aunque eran conocidos desde tiempo inmemorial.
Esta es una representación antigua de estos cinco poliedros en el libro de Kepler (1571-1630)
"Harmonices Mundi" ("La harmonía del mundo"). En esta ilustración se muestran los poliedros y su asociación con los
cuatro elementos. El tetraedro con el fuego, el octaedro con el aire, el cubo con la tierra y el icosaedro con el
agua. El dodecaedro estaría asociado con el universo o cosmos.
Es muy instructivo construir estos cinco sólidos platónicos y aquí pretendemos animar a realizar
esta actividad. En esta página se muestran ejemplos de construcciones
con diferentes técnicas.
Estos poliedros platónicos forman parte de una colección que fue hecha en la década de los treinta del siglo pasado:
La regularidad se concreta en dos exigencias:
Todas sus caras son congruentes (iguales) y tienen que ser un polígono regular.
Todos los vértices tienen que ser iguales. En cada vértice tienen que concurrir el mismo número de caras y, por lo tanto, también el mismo
número de aristas.
Resulta que estos polígonos regulares que forman las caras de cada sólido platónico sólo pueden ser triángulos
equiláteros, cuadrados y pentágonos.
Sólo se pueden construir cinco sólidos con estas características. Las caras de tres de ellos son triángulos equiláteros
(el tetraedro, el octaedro y el icosaedro), el cubo tiene las caras cuadradas y el dodecaedro tiene sus caras que son
pentágonos regulares.
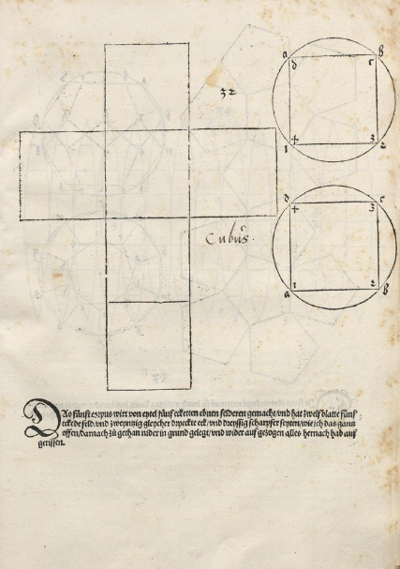
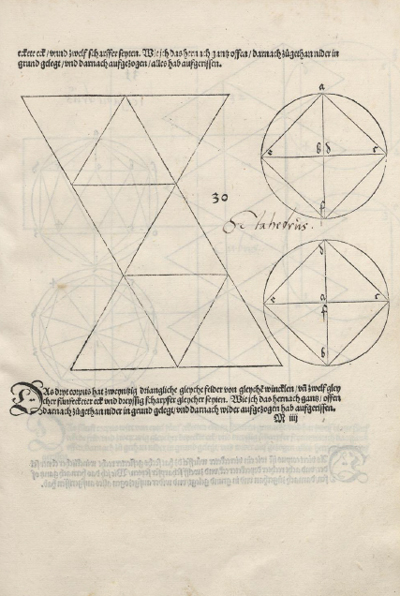
Un modo de construir estos poliedros es a partir de su desarrollo plano. Alberto Durero es el primero en publicar
desarrollos planos de varios poliedros, entre ellos, los platónicos. Las ilustraciones de estos desarrollos son de su libro
"Underweysung der Messung" ("Tratado de la medida", 1525).
Vamos a ver estos poliedros y contar sus elementos:
Tetraedro
Las caras del tetraedro son triángulos equiláteros.
Podemos decir que diferentes técnicas de construcción se fijan en elementos particulares de las figuras. Por ejemplo,
para hacer esta construcción del tetraedro con bolitas necesitamos cuatro bolas que se corresponden con los vértices de la figura.
El tetraedro es un poliedro sencillo y es fácil contar sus caras, aristas y vértices:
PARA SABER MÁS

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
Cubo
Estamos muy familiarizados con el cubo. Sus caras son cuadrados y todos sabemos que un dado tiene 6 caras.
Contamos las caras, aristas y vértices del cubo:
Octaedro
Las caras del octaedro son triángulos equiláteros.
Contamos las caras, aristas y vértices del octaedro:
PARA SABER MÁS

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.

El primer dibujo del desarrollo plano del octaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro.
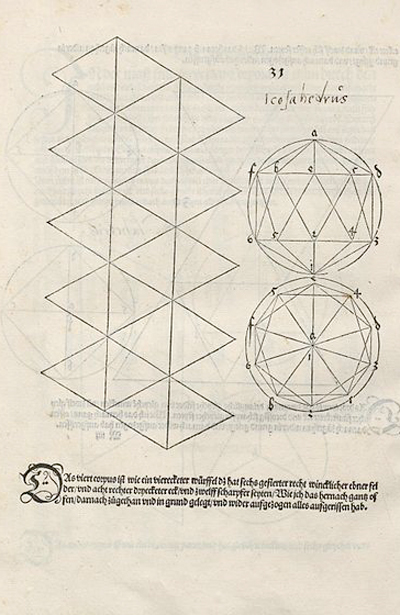
Icosaedro
El icosaedro tiene 20 caras triángulares. Su desarrollo nos lo mostró Durero:
Los poliedros formados por triángulos, como el icosaedro, el tetraedro y el octaedro, tienen la particularidad de que si se
construyen uniendo varillas, la estructura resultante es rígida. Este hecho tiene aplicaciones en arquitectura e ingeniería.
Otro ejemplo de este tipo de estructuras son las cúpulas geodésicas.
¿Cómo podemos contar las aristas y los vértices de un icosaedro sin dejarnos ninguno? Hay un truquillo.
La técnica de construir poliedros recortando cada cara por separado y después pegando las caras o uniéndolas con gomas nos va a
ayudar.
Para hacer un icosaedro necesitamos 20 triángulos equiláteros. Estos triángulos tienen 60 aristas y 60 vértices.
Pensemos primero en las aristas. Estas 60 aristas de triángulo se pegan de 2 en 2 para formar una arista del icosaedro,
por lo tanto, ya sabemos el número de aristas de un icosaedro.
En un vértice del icosaedro se juntan 5 vértices de triángulos. Esto nos dice el número de vértices del icosaedro.
PARA SABER MÁS

Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.

Con tres rectángulos áureos podemos construir un icosaedro.
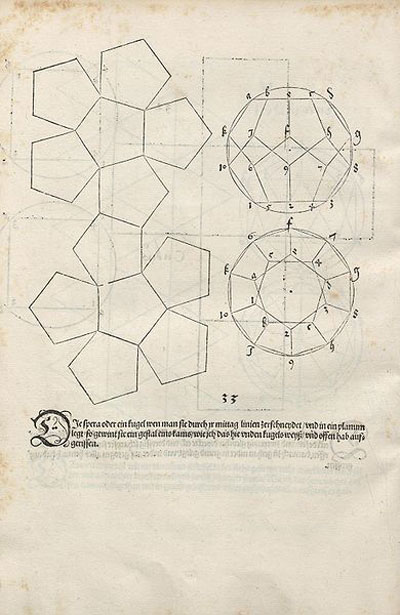
Dodecaedro
Contamos las caras, aristas y vértices del dodecaedro. Podemos usar el truquillo que hemos empleado para el
icosaedro.
PARA SABER MÁS

Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.
INVESTIGA
La unión de dos tetraedros es un poliedro formado por seis triángulos equiláteros.
¿Por qué la unión de dos tetraedros no se considera un sólido platónico?
INVESTIGA
En este breve repaso de los poliedros podríamos citar a muchas personas que hicieron contribuciones.
Por lo menos, a Platón, Euclides, Arquímedes, Pacioli, Durero, Kepler entre otros muchos más.
Un cambio crucial en cómo vemos los poliedros lo asociamos a Euler. Euler considera que un poliedro está formado por vértices
(elementos de dimensión 0), aristas (dimensión 1) y caras (dimensión 2).
Con este cambio de punto de vista deduce la famosa Fórmula de Euler: Caras menos Aristas más Vértices es igual a 2.
Esta fórmula es válida para los poliedros que 'se parecen a esferas', en particular no deben tener agujeros.
Los poliedros platónicos y los arquimedianos, en particular, la cumplen.
Una consecuencia de este punto de vista es que podemos considerar ciertas deformaciones del poliedro y la fórmula se sigue verificando pues
lo importante no es que las aristas sean rectas o que tengan tales o cuales medidas. Podemos imaginar la figura hecha de goma y estirando
(sin rasgar) deformamos el poliedro pero la fórmula se seguirá cumpliendo. Estas ideas
(junto con el problema de los Puentes de Koningsberg -que resolvió Euler-) están en el origen de una
rama de las Matemáticas que llamamos
Topología.
Repasar el número de vértices, aristas y caras de los sólidos platónicos y comprobar que se cumple la Fórmula de Euler.
INVESTIGA
La demostración de que hay solo cinco sólidos platónicos no es tan simple.
Se suele apoyar en la fórmula de Euler para los poliedros (que, por cierto, también está relacionada con los mapas y con el
problema de los cuatro colores)
Para empezar se rebajan las condiciones de la definición de poliedro regular. Diremos que un poliedro es regular si
todas sus caras tienen el mismo número de lados y si en cada vértice se une el mismo número de caras.
Por lo tanto, no se exige que las caras sean polígonos regulares.
En estas condiciones, viendo las posibilidades de recuento de caras, aristas y vértices se prueba que, como mucho, hay cinco
posibilidades.
Entonces, si consideramos que las caras tienen que ser polígonos regulares, tenemos que construir los cinco sólidos platónicos
usando geometría métrica.
Un modo sería definir los vértices y comprobar que todas las aristas son de la misma longitud y todos los ángulos en los
vértices son iguales.
Para ver los detalles se puede consultar los libros de Rademacher y Toeplitz (capítulos 12 y 13) y el de Cromwell.
REFERENCIAS
Peter R. Cromwell - Polyhedra, Cambridge University Press, 1999.
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition. (Versión en castellano publicada por
Salvat 'Instantáneas matemáticas', 1986).
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
 SIGUIENTE
SIGUIENTE

Estudiamos el concepto de dualidad de poliedros aplicado a los sólidos platónicos. El cubo y el octaedro son duales, el icosaedro y el dodecaedro son duales y el tetraedro decimos que es autodual.
MÁS ENLACES

Material para la sesión sobre construcción de poliedros que se realizó en Zaragoza el 13 de Abril de 2012. El objetivo es disfrutar haciendo poliedros y obtener alguna conclusión matemática a partir de esas construcciones.

Material para la sesión sobre construcción de poliedros (Zaragoza el 9 de Mayo de 2014). Empezaremos con el tetraedro, el cubo y el octaedro y presentaremos el cuboctaedro y el dodecaedro rómbico. Relacionaremos este poliedro con los panales de abeja. Construimos una cajita que es un dodecaedro rómbico.

Material para la sesión sobre poliedros (Zaragoza el 7 de Noviembre de 2014). Estudiaremos el volumen del octaedro y del tetraedro y veremos que el octaedro truncado nos puede ayudar en esta tarea. Construimos una cubo de cartulina con un tetraedro de origami modular en su interior.

Material para la sesión del TTM (Zaragoza el 23 de Octubre de 2015) . Estudiamos la dualidad de poliedros y, en particular, los poliedros platónicos duales. Construimos una cubo de cartulina con un octaedro de origami modular.

Material para la sesión del TTM (Zaragoza, el 21 de Octubre de 2016). Con plantillas para descargar y construir varias figuras geométricas.

Material para la sesión del TTM (Zaragoza, el 20 de Octubre de 2017). El objetivo principal es disfrutar con las Matemáticas y fomentar la construcción de poliedros por su valor estético y también porque nos facilitan la comprensión de resultados matemáticos.

Material para la sesión del TTM (Zaragoza, el 19 de Octubre de 2018). Diferentes construcciones del icosaedro nos ayudan a comprender sus propiedades. El objetivo principal es disfrutan construyendo poliedros.

Material para la sesión del TTM (Zaragoza, el 18 de Octubre de 2019). El objetivo principal es disfrutan construyendo poliedros, en esta ocasión construiremos una cajita que es un dodecaedro rómbico. Estudiaremos la relación de este poliedro con el cubo, el octaedro y el cuboctaedro.

Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

Podemos dibujar los desarrollos planos en cartulina y construir poliedros uniendo solapas con pegamento.

Si recortamos las caras sueltas de los poliedros podemos unirlas con gomas elásticas o pegamento y construir poliedros más complicados y con varios colores.

Si recortamos las caras sueltas de los poliedros podemos unirlas con pegamento y construir poliedros. Puedes descargar varias plantillas con diferentes polígonos. Es una técnica muy sencilla para construir poliedros muy vistosos e interesantes.

Técnica simple para construir poliedros pegando discos de cartulina.

El diseñador italiano Bruno Munari pensó 'Acona Biconbi' como un trabajo de escultura. También es un juego de construcción con el que podemos jugar con colores y formas.

Tubos de plástico o aluminio unidos son muy útiles para construir esqueletos de poliedros.

Con tres rectángulos áureos podemos construir un icosaedro.

El origami modular es una técnica preciosa que consiste en plegar varias unidades independientes que se unen sin pegamento para formar poliedros.

Tensegrity es la construcción de estructuras con tensores o elementos elásticos. Es un placer construir y tocar estos poliedros elásticos.

Zome es un conjunto de piezas de plástico ideal para construir poliedros desmontables. De las infinitas posibilidades de Zome, aquí lo usamos para calcular el volumen del dodecaedro.

Construcción del tetraedro con impresión 3d. El tetraedro es un poliedro autodual. El centro del tetraedro.

Construcción del cubo y del octaedro con impresión 3D. El cubo y el octaedro son poliedros duales.

Microarquitectura es un juego de construcción desarrollado por Sara San Gregorio. Podemos jugar con él y construir muchas estructuras inspiradas en poliedros.

El volumen del tetraedro es un tercio del paralelepípedo que lo contiene.

El primer dibujo del desarrollo plano del tetraedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

El volumen del octaedro es 4 veces el del tetraedro. El cálculo del volumen del octaedro es sencillo y así podemos obtener el volumen del tetraedro.

El primer dibujo del desarrollo plano del octaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su octaedro.

Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.

Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.

























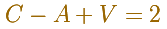
 SIGUIENTE
SIGUIENTE












































