En esta página continuamos el estudio de la interpretación geométrica de los números complejos como puntos (o vectores) en el plano.
"La publicación de la interpretación geométrica por Wessel y por Argand no estuvo muy difundida, pero la reputación de Gauss (tan grande entonces como ahora) aseguró una amplia difusión y aceptación de los números complejos como puntos en el plano. Quizás menos importante que los detalles de esta nueva interpretación (al menos, inicialmente) fue el hecho de que ahora existía un modo de dar sentido a estos números -que ahora eran objetos legítimos de investigación. De cualquier manera, las puertas de la invención se abrieron de par en par." (Needham, 3)
En concreto, vamos a seguir con la relación que hay entre la multiplicación de complejos y la transformación que conocemos como rotación dilatativa.
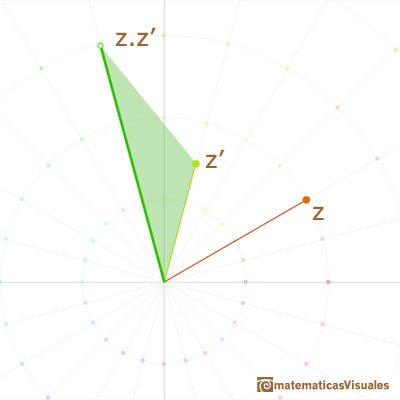
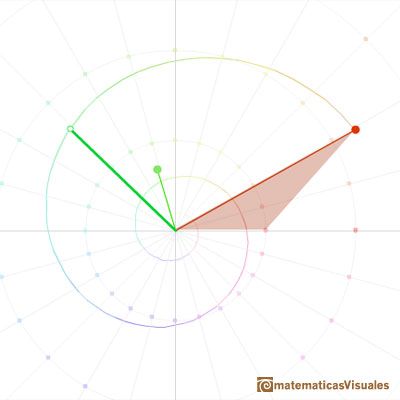
Geométricamente, la multiplicación por un número complejo z es una rotación del plano (el ángulo de rotación es el argumento de z y una expansión (o contracción) del plano por un factor que es el módulo o longitud de z. El origen no cambia.
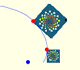
Si usamos la técnica de Frank Farris de representar el plano complejo con colores podemos ver una representación inicial:
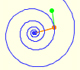
Y la representación del plano después de multiplicar por un número complejo z.
Rotaciones y expansiones preservan paralelogramos. En particular, vemos que un cuadrado se transforma en otro cuadrado.
REFERENCIAS
SIGUIENTE
ANTERIOR
MÁS ENLACES
