La función

es distinta de la función exponencial o de la función seno en el sentido de que esta función no está definida para todos los valores (su dominio no es la recta real entera), entonces no tiene sentido decir que un polinomio (o una serie infinita) se aproxima a la funcíón para todos los valores de x o que la serie converge para todos los valores.

Podemos calcular la serie de potencias en x = 0 fácilmente, usando el Teorema del Binomio de Newton, pero la función no está definida cuando x es menor que -1.

Nuestro interés se centrará en estudiar qué ocurre cuando x es mayor o igual que -1.

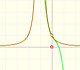
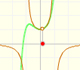
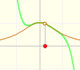
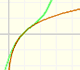
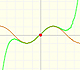
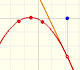
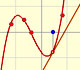
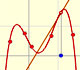
"En el intervalo (-1, +1) las parábolas aproxima a la curva original más y más conforme el orden aumenta; pero a la derecha de x = 1 se desvían de ella cada vez más, ahora por arriba, ahora por abajo, de un modo sorprendente." (Felix Klein)

Decimos que este intervalo (-1, +1) es el círculo o intervalo de convergencia de la serie de potencias. Es un comportamiento típico que una serie de potencias converga dentro de un intervalo de convergencia y diverja fuera del círculo. Entenderemos mejor este comportamiento y el uso de la palabra 'círculo' cuando estudiemos el plano complejo.

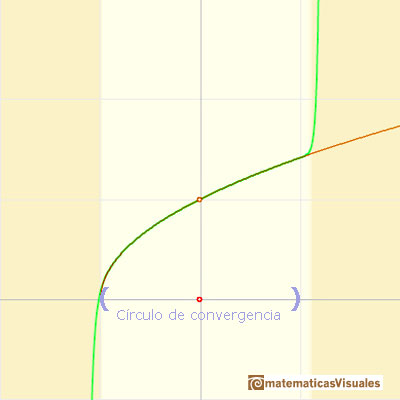
Es interesante estudiar qué ocurre en la frontera, es decir en los puntos x = -1 y x = 1. En el punto x = -1, la rama de la curva original que aparece en el dibujo termina en una tangente vertical "todas las parabolas se extienden más allá de este punto pero aproximan a la curva original más y más en x = -1, volviendose cada vez más empinadas". En el punto x = +1, simétrico de x = -1, las parábolas aproximan la curva original cada vez con mayor precisión también.

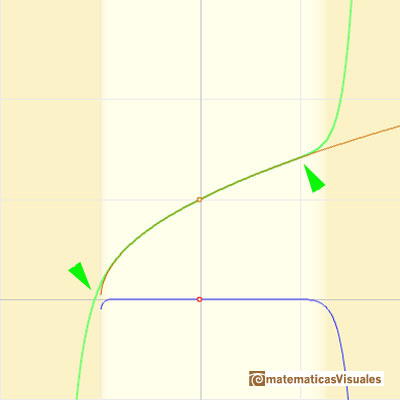
Podemos ver qué ocurre con alguna función con singularidades, por ejemplo, Polinomios de Taylor (4): función racional 1.

REFERENCIAS

MÁS ENLACES

Polinomios de Taylor (5): función racional 2

La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.

Polinomios de Taylor (6): función racional con 2 singularidades

La función tiene dos singularidades reales, en -1 y en 1. Los polinomios de Taylor aproximan la función entre en un intervalo simétrico respecto al centro del desarrollo. Su radio es la distancia a la singulardidad más próxima.

Polinomios de Taylor (7): función racional sin singularidades reales

La función es continua y no tiene singularidades reales. Sin embargo, los polinomios de Taylor sólo aproximan la función en un intervalo. Entenderemos un poco mejor este comportamiento estudiando una función compleja.

Mercator y Euler: La función logaritmo

Mercator publicó su famosa serie para la función logaritmo en 1668. Euler descubrió una serie práctica para el cálculo.

Polinomios de Taylor (1): función exponencial

Al aumentar el grado del polinomio de Taylor se aproxima a la función exponencial en un intervalo más y más amplio.

Multifunciones: Potencias con exponente fraccionario

El concepto de función puede extenderse permitiendo que f(z) tenga diferentes valores para un valor z. En este caso decimos que f es una función multivaluada o multifunción.

Funciones polinómicas y derivada (1): Funciones afines

La derivada de una función lineal es la función constante cuyo valor es la pendiente de la recta.

Funciones polinómicas y derivada (2): Funciones cuadráticas

La derivada de una función cuadrática es una función afín, es decir, es una línea recta.

Funciones polinómicas y derivada (3): Funciones cúbicas

La derivada de una función cúbica es una función cuadráticas, es decir, una parábola

Funciones polinómicas y derivada (4): Polinomios de Lagrange (funciones polinómicas en general)

Los polinomios de Lagrange son polinomios que pasan por n puntos dados. Usamos los polinomios de Lagrange para explorar funciones polinómicas más generales y sus derivadas.