Una función cúbica es una función polinómica de grado 3. Las funciones cúbicas tienen expresiones del tipo:
Estamos interesados en estudiar la derivada de funciones simples con un punto de vista intuitivo y visual. Para estudiar la derivada de una función cúbica vamos a seguir la misma aproximación que hemos usado para el caso de las funciones cuadráticas.
EL CONCEPTO DE DERIVADA DE UNA FUNCIÓN
La derivada de una función en un punto puede definirse como la tasa de variación instantánea o como la pendiente de la recta tangente a la gráfica de la función en ese punto. Podemos definir la pendiente de la función en un punto como la pendiente de la recta tangente.
La pendiente de la tangente depende, en general, de x. Entonces, a partir de una función podemos definir una nueva función, la función derivada de la función original.
El proceso de encontrar la función derivada de una función se llama diferenciación.
El valor de la función derivada para cada valor de x es la pendiente de la función original en x.
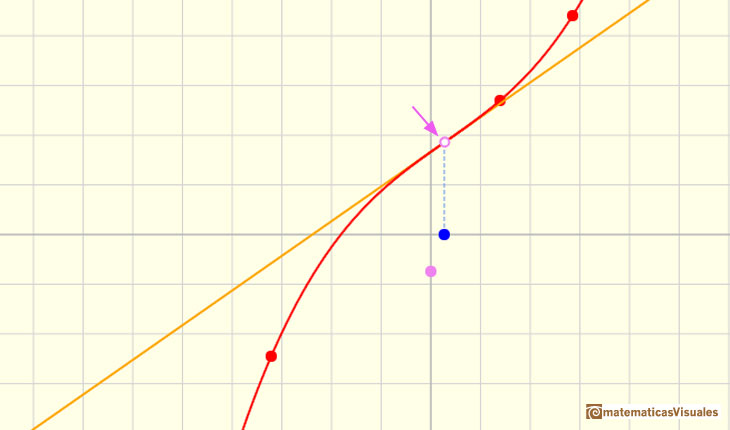
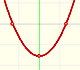
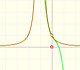
Si la derivada de una función en un punto es la pendiente de la recta tangente en ese punto, para representar la derivada en un punto nos podemos plantear dibujar la recta tangente a la gráfica de una función cúbica en ese punto:
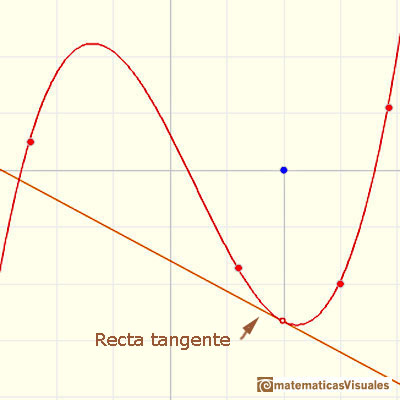
Pero, ¿cómo podemos dibujar la tangente? De momento solo lo podemos hacer aproximadamente, un poco a ojo. Para mejorar la precisión podemos usar una lupa. Si miramos muy cerca el punto en la gráfica de la función podemos ver cómo la recta tangente es muy semejante a la función. La recta tangente es la mejor aproximación lineal de la función en ese punto:
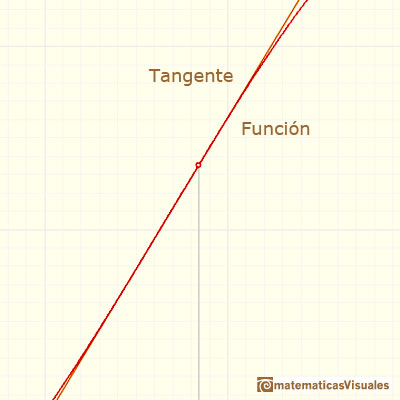
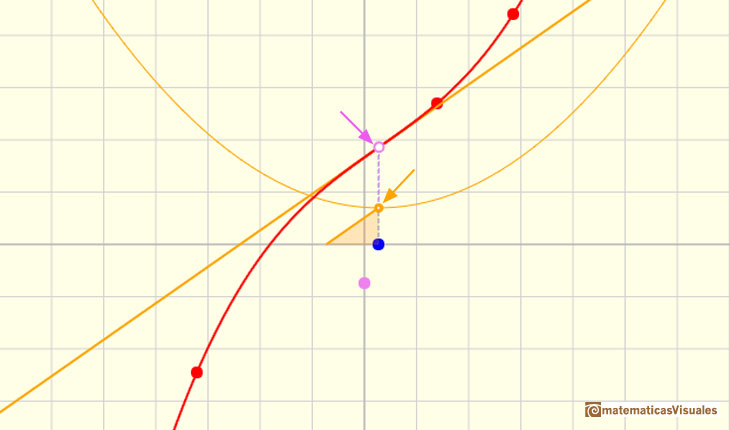
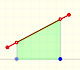
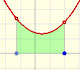
Para calcular la pendiente de esa recta podemos usar varias técnicas. Una de ellas es dibujar una recta paralela a esa tangente a través del valor x-1 y obtener un triángulo rectángulo. La longitud del lado vertical de este triángulo es el valor de la pendiente de la tangente y, por lo tanto, el valor (aproximado) de la derivada de la función en ese punto.
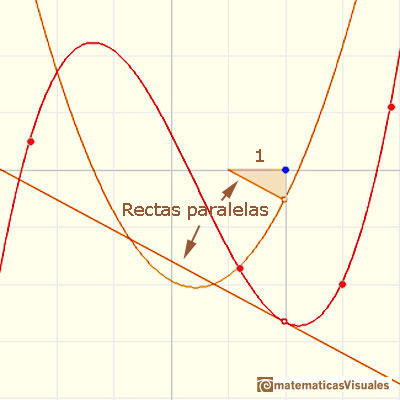
Si hiciéramos este laborioso proceso en muchos puntos de la función podríamos ver que los valores de la derivada así construída se aproximan a una curva conocida, una parábola. Realmente la derivada de una función cúbica es una función cuadrática.
La regla de derivación de una función cúbica la aprendemos cuando empezamos a derivar y es la siguiente:
Es una herramienta muy potente pues nos permite calcular la derivada de la función en un punto con mucha facilidad. En particular, desde un punto de vista gráfico, nos permitirá dibujar la recta tangente con precisión pues podremos conocer la fórmula exacta de la recta tangente.
En nuestro caso, la derivada de una función cúbica es una parábola. Vamos a ver cómo nuestro conocimiento de las parábolas nos va a dar información muy importante sobre la función cúbica de partida.
Sabemos que algunas funciones cúbicas tienen montañas y valles y que la 'cima de la montaña' es un máximo local y que el 'fondo del valle' es un mínimo local.
Si pensamos en las tangentes vemos que en esos puntos la función ni crece ni decrece, su tangente es horizontal.
Un punto crítico de una función polinómica es un punto en el que la tangente es paralela al eje de abcisas (eje x). Es decir, que la pendiente de la recta tangente en ese punto es 0.
Por lo tanto, el máximo y el mínimo local (si existen) son puntos críticos. Al revés no es cierto: puede haber puntos con derivada 0, con recta tangente horizontal, que no sean ni máximo ni mínimo. Eso lo veremos un poco más adelante.
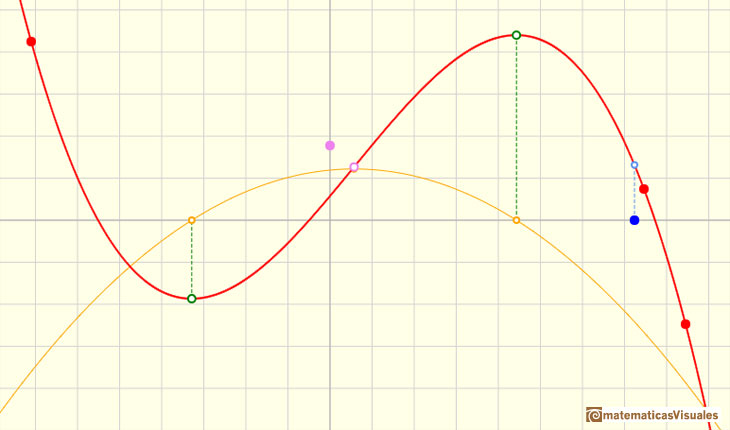
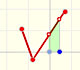
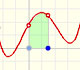
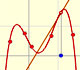
En el siguiente ejemplo podemos ver una función cúbica con dos puntos críticos. Uno es un máximo local y el otro es un mínimo local.
Si pensamos en la función derivada, la parábola, lo que estamos buscando son los valores en los que la función derivada se hace 0, en los que la parábola corta al eje de las x.
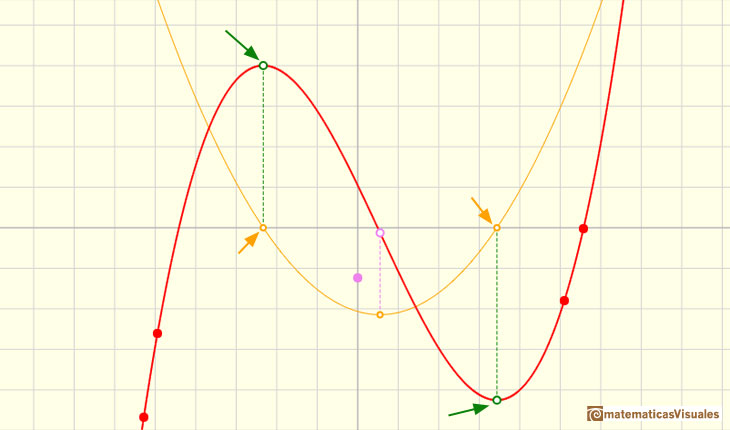
Esos valores son las coordenadas x de los puntos críticos de la función, con sus tangentes horizontales. Son los candidatos a máximo y mínimo local.
Para encontrar los puntos críticos podemos resolver la ecuación cuadrática:
En este caso, las soluciones de esta ecuación son:
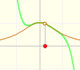
Como ya sabemos (funciones cuadráticas), algunas ecuaciones cuadráticas no tienen soluciones reales (la parábola no corta al eje de las x). En estos casos la función cúbica no tiene puntos críticos:
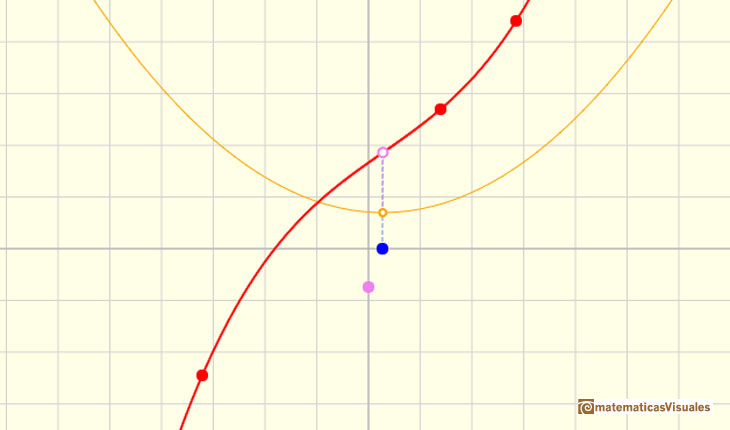
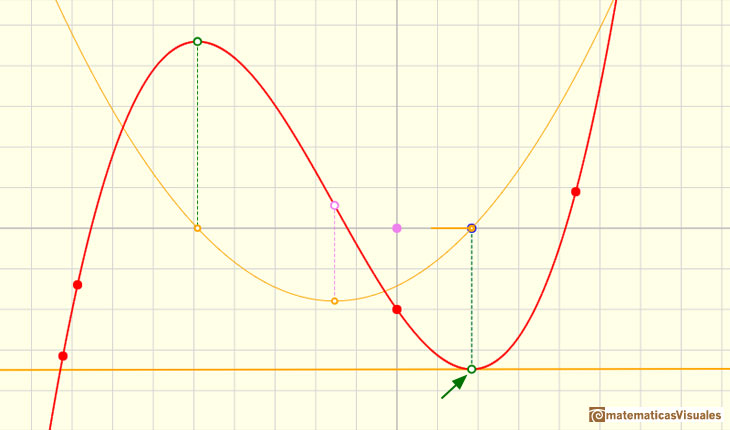
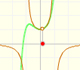
Pero una parábola siempre tiene un vértice. El vértice de la parábola está relacionado con un punto de la función cúbica. Llamamos a este punto un punto de inflexión.
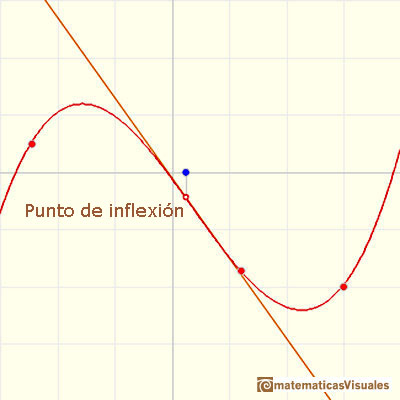
Un punto de inflexión de una función cúbica es el único punto de la gráfica en el que cambia la concavidad.
La curva cambia de ser cóncava hacia arriba a ser cóncava hacia abajo, o viceversa.
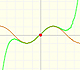
La recta tangente a una función cúbica en el punto de inflexión cruza la gráfica:
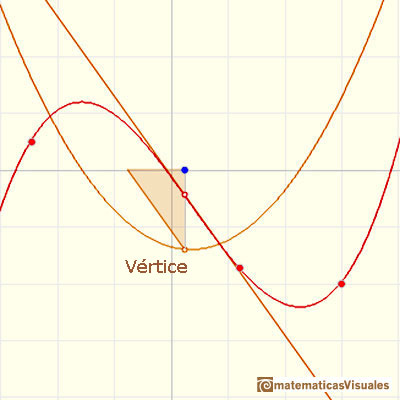
Para calcular el punto de inflexión podemos calcular el vértice de la parábola:
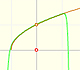
Este es un ejemplo de un punto de inflexión de una función cúbica que no tiene puntos críticos:
Vemos cómo la recta tangente corta a la gráfica de la función:
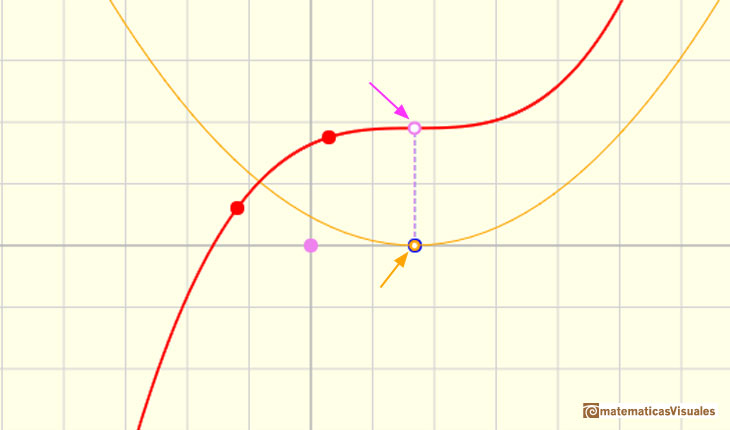
Hemos visto que cuando la derivada (la parábola) corta al eje de abcisas en dos puntos tenemos dos puntos críticos que son el máximo y el mínimo local de la cúbica y, además, hay otro punto especial, que se corresponde con el vértice de la parábola, que es el punto de inflexión.
Cuando la parábola no corta al eje de las x no tenemos puntos críticos y tampoco máximo ni mínimo local. Pero siempre tenemos un vértice que se corresponde con el punto de inflexión. En este caso la ecuación de la parábola no tiene raíces reales.
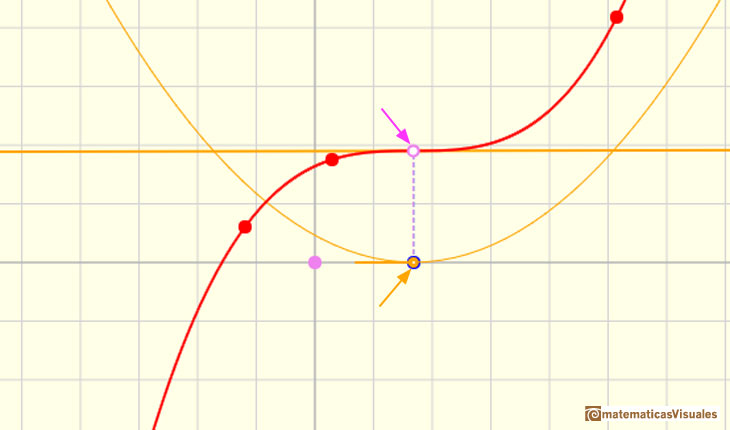
Hay un caso especial que es cuando la parábola toca al eje de las x en el vértice. En este caso, la parábola solo tiene una raíz real (que consideramos doble). Podemos pensar que estos tres puntos especiales de la parábola (los dos ceros y el vértice) se han confundido en uno solo. Entonces el punto de inflexión de la función cúbica es un punto crítico, la pendiente de la tangente en este punto es 0 pero este punto crítico no es un máximo ni un mínimo local. La función cúbica no tiene máximo ni mínimo local y será creciente o decreciente en todo su dominio.
El punto de inflexión en el siguiente ejemplo es también un punto crítico (observamos que el vértice de la derivada toca al eje de abcisas).
Un punto de inflexión puede ser un punto crítico, pero no es un máximo o mínimo local.
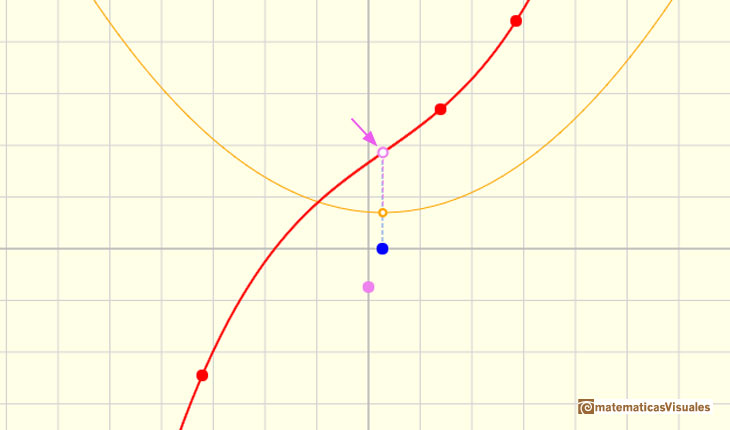
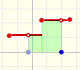
Una idea simple e interesante es que cuando trasladamos arriba y abajo el gráfico de la función (sumamos o restamos un número a la función original) la función derivada no cambia. La razón es muy intuitiva. Cuando movemos el punto violeta trasladamos verticalmente la función y la función derivada no cambia:
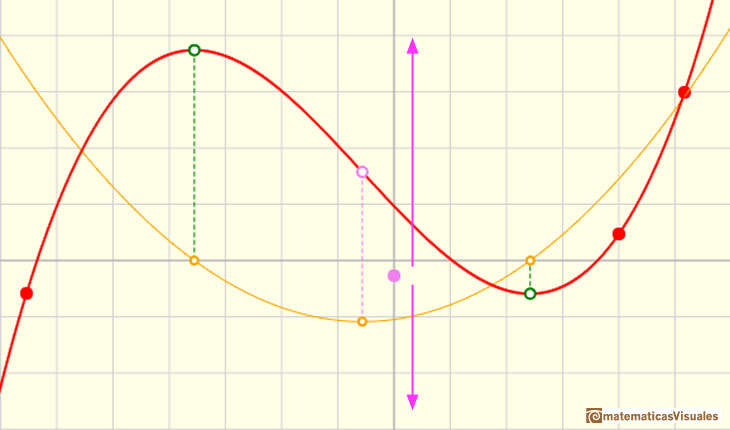
Es importante notar que la derivada de un polinomio de grado 1 es una función constante (un polinomio de grado 0). La derivada de un polinomio de grado 2 es un polinomio de grado 1. Y que la derivada de un polinomio de grado 3 es un polinomio de grado 2.
Cuando derivamos esas funciones polinómicas el resultado es un polinomio de un grado menor que la función original.
Cuando estudiamos la integral de un polinomio de grado 2 veremos que en este caso la nueva función es un polinomio de grado 3. Un grado más que la función original.
Estos resultados están relacionados con el Teorema Fundamental del Cálculo.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
MÁS ENLACES























 ANTERIOR
ANTERIOR