Funciones potencia
Las funciones potencia básicas son
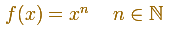
El número n se llana exponente. Empezamos estudiando funciones potencia con exponente un número natural (un entero positivo). La expresión xn la podemos leer como 'x elevado a n' o 'x elevado a la potencia n'.
Esta familia de funciones incluye alguna línea, parábola, parábola cúbica, etc.
Son la base de las funciones polinómicas.
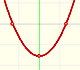
Son ejemplos de funciones pares e impares. El eje Y de una función par es un eje de simetría de la función: el eje Y hace de espejo y la mitad de su gráfica es una imagen especular de la otra mitad. Si el exponente de una funcion potencia es par, entonces la función es par:
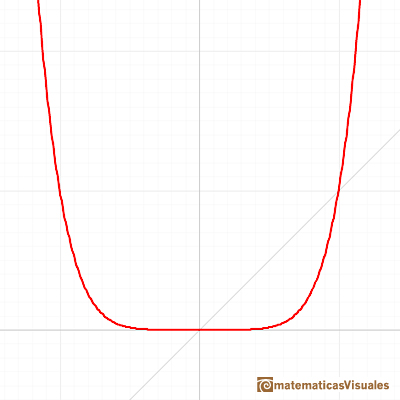
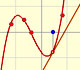
Algunas funciones son simétricas respecto del origen. Decimos que son funciones impares. Si el exponente de una función potencia es impar, entonces la función es impar:
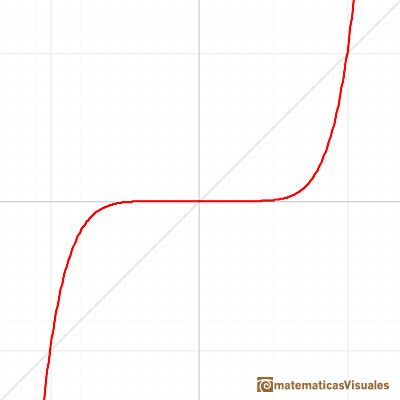
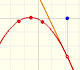
Las funciones potencia pares e impares tienen un comportamiento diferente cuando x se hace grande en módulo (positivo o negativo, hacia la derecha y hacia la izquierda).
Viendo el vídeo podemos aceptar (intuitivamente) estos límites:

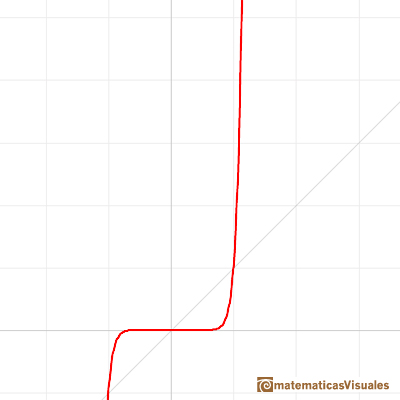
La inversa de las potencias es extraer una raíz (funciones raíz n-ésima):
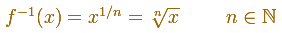
Las funciones raíces son funciones potencia con exponente el inverso de un entero positivo (n se dice el índice de la raíz).
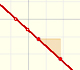
Una función y su inversa son simétricas respecto a la diagonal del primer cuadrante. Obtenemos la gráfica de una función inversa reflejando la gráfica respecto de la recta y=x.
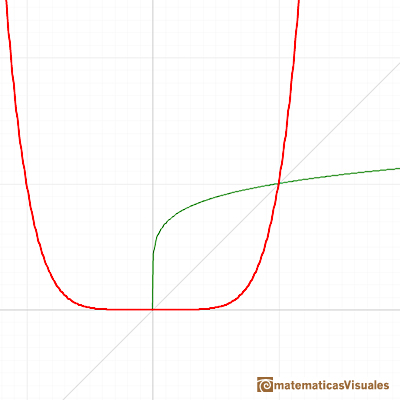
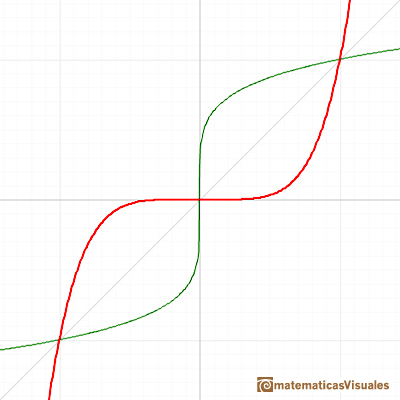
El dominio de estas funciones es todos los números reales si n es impar y sólo los reales no negativos si n es par.
Viendo el applet podemos aceptar (intuitivamente) este límite:
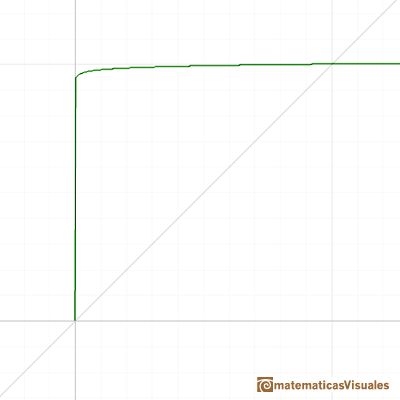
El siguiente paso es considerar funciones potencia con exponente un número racional positivo:
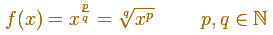
REFERENCIAS
Richard Courant y Fritz John - Introducción al cálculo y al análisis matemático. Ed. Limusa-Wiley.
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES
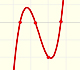
Las funciones cúbicas son polinomios de grado 3. Una función cúbica real siempre corta al eje de abcisas por lo menos una vez.

Se trata de encontrar el polinomio de menor grado que pasa por una serie de puntos del plano. Es un problema de interpolación que aquí resolvemos usando los polinomios de Lagrange.
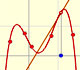
Los polinomios de Lagrange son polinomios que pasan por n puntos dados. Usamos los polinomios de Lagrange para explorar funciones polinómicas más generales y sus derivadas.
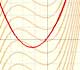
Si la derivada de F(x) es f(x) decimos que F es una antiderivada de f. También decimos que F es una primitiva o una integral indefinida de f.

La integral formaliza el concepto intuitivo de área. Para su definición aproximamos el área usando rectángulos.

Las funciones monótonas definidas en intervalos cerrados son interables. En estos casos podemos acotar el error que cometemos al aproximar la integral usando rectángulos.

Si consideramos el límite inferior de integración fijado y podemos calcular la integral definida para diferentes valores del límite superior de integración entonces podemos definir una nueva función: una integral indefinida de f.

Es fácil calcular el área bajo una línea recta y el eje de abcisas. Es un primer ejemplo de integración que nos permite entender la idea e introducir algunos conceptos básicos: integral como área, límites de integración, áreas positivas y negativas.
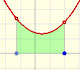
Calcular el área bajo una parábola es mucho más difícil que calcular áreas bajo una recta. Aquí mostramos como aproximar el área usando rectángulos y que una función integral de un polinomio de grado 2 es un polinomio de grado 3.
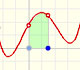
Estudiamos algunos conceptos básicos sobre integración aplicados a funciones polinómicas de cualquier grado. Las funciones integrales de funciones polinómicas son polinomios de un grado más que la función original.

El Teorema Fundamental del Cálculo afirma que toda función continua tiene una antiderivada y nos muestra cómo construir una usando la integral.

El Segundo Teorema Fundamental del Cálculo nos proporciona una herramienta muy potente para calcular integrales definidas (si conocemos una primitiva o antiderivada de la función).
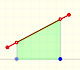
Como una introducción a las funciones lineales a trozos estudiamos el caso más sencillo, las funciones lineales restringidas a un intervalo abierto: sus gráficas son segmentos.
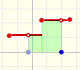
Una función constante a trozos (o función escalonada) está definida por varias subfunciones que son funciones constantes.
Una función continua lineal a trozos se define con varios segmentos o rayos que están unidos de un modo continuo, sin saltos entre ellos.

Un polinomio de grado 2 tiene dos raíces o ceros. En esta representación podemos ver los óvalos de Cassini y la lemniscata.

Un polinomio de grado 3 tiene tres ceros o raíces. Podemos modificar los tres ceros de este tipo de polinomios.