Ya hemos estudiado el ejemplo más básico de funciones definidas a trozos: las funciones escalera (o escalonadas).
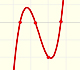
Ahora vamos a estudiar funciones definidas a trozos pero cuyos trozos no tienen que ser necesariamente constantes. Empezamos por las funciones lineales a trozos que, además, son continuas. Las funciones lineales a trozos pueden tener alguna discontinuidad en los extremos de los subdominios que definen la función. En el caso que consideramos en esta página las funciones son continuas y su gráfico está formado por segmentos rectos unidos.
Las funciones continuas lineales a trozos F y las funciones escalera f están emparejadas de alguna manera.
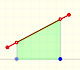
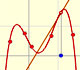
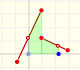
Hacemos un uso típico de las funciones continuas lineas a trozos cuando unimos varios puntos de una gráfica usando segmentos. Este tipo de aproximación a una gráfica se llama interpolación lineal.
Un ejemplo de función continua lineal a trozos es la definición de la función valor absoluto.
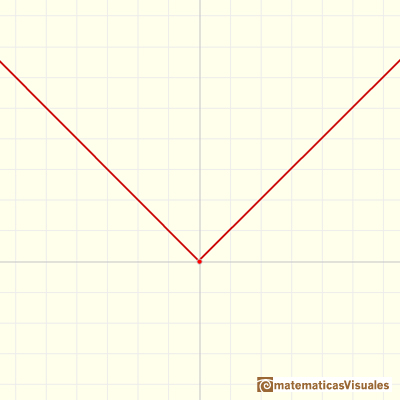
Si consideramos ahora la derivada de cada trozo (en este caso sencillo, la derivada es la pendiente de una linea recta) obtenemos una función escalonada.
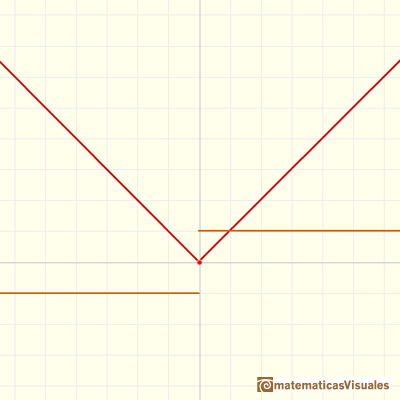
Es interesante destacar que estas funciones continuas son 'suaves en casi todas partes'. Solo puede haber algunos puntos en los que la función no sea suave. Tienen unos pocos 'picos'. Podemos decir que son ejemplos de funciones diferenciables a trozos (o que son 'diferenciables en casi todas partes').
Una función es diferenciable a trozos si es diferenciable en una serie de subdominios aunque la función en su conjunto no sea diferenciable. En estos casos vemos que la función deja de ser diferenciable en los extremos de los subdominios de definición.
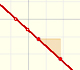
Recordamos que el gráfico de una función lineal es una linea recta.
La derivada de una función lineal es el ejemplo más básico de derivada pues es una función constante.
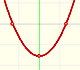
La integral de una función lineal no constante es una función cuadrática.

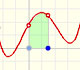
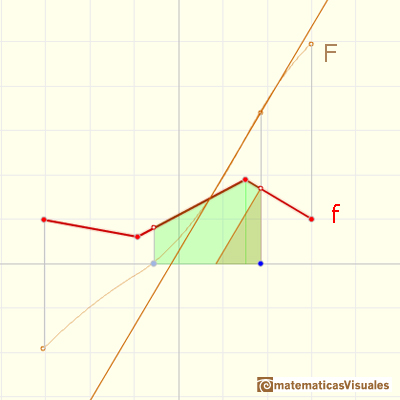
Ahora nos vamos a fijar en la relación entre una función continua lineal a trozos F y la función escalonada f que podemos definir con las pendientes de cada trozo de F.
Podemos considerar una función F:
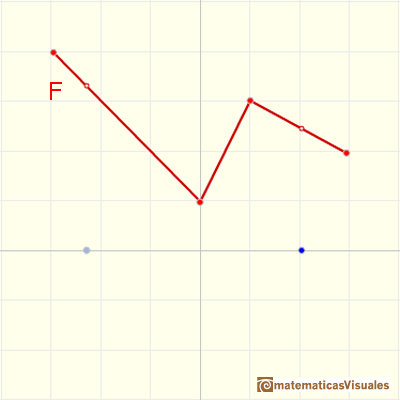
Entonces las pendientes definen una función escalonada f (y podemos ver esta función como 'velocidad'):
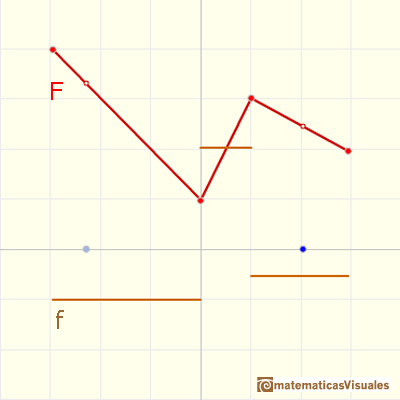
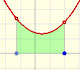
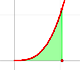
Si ahora queremos calcular el área bajo esta función escalonda f ...
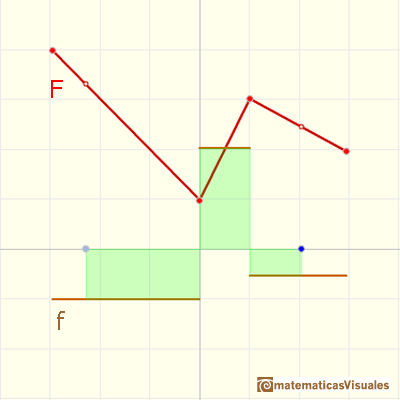
... obtenemos una función lineal a trozos que es una traslación vertical de la función a trozos original.
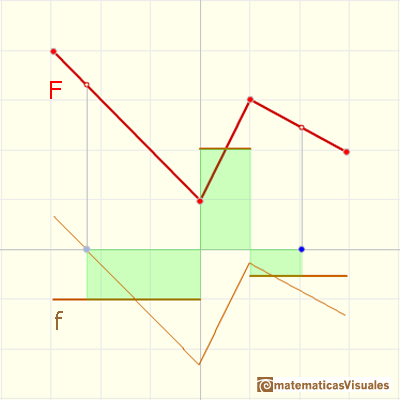
Este proceso se llama integración. En este caso es sencillo pues se trata de calcular áreas de rectángulos. La función que obtenemos es una función integral (que la podemos interpretar como 'distancia', si f es la 'velocidad').
Cambiando el origen de integración (el punto azul lo podemos mover de derecha a izquierda) trasladamos la función integral arriba y abajo.
En el siguiente vídeo empezamos con una función escalonada f y buscamos una función continua a trozos F cuyas pendientes sean iguales a la función escalonada inicial. A este proceso también lo llamamos integración.
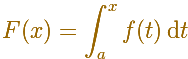
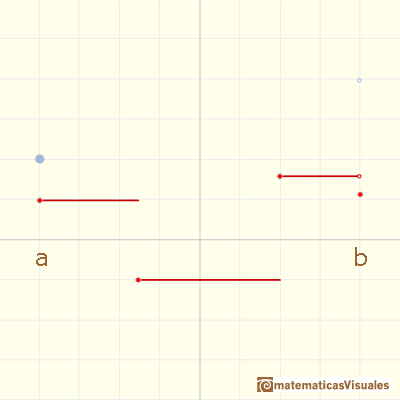
Podemos arrastrar arriba y abajo el punto azul para la traslada la función integral: hay infinitas funciones integrales.
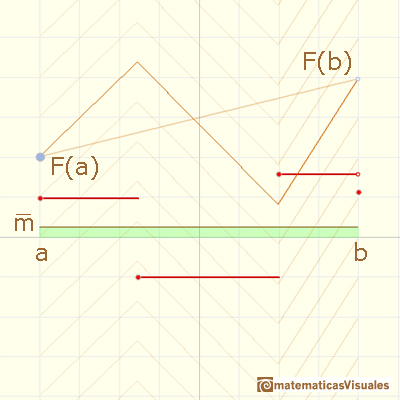
Si F(a) está fijado podemos considerar la función F(x)
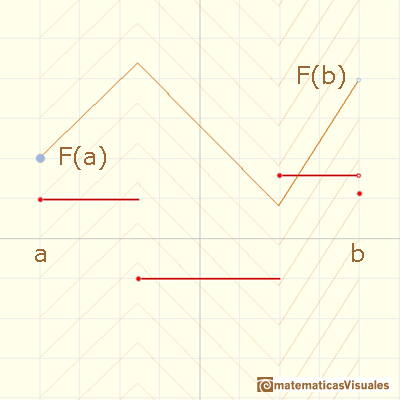
Supongamos que nos interesa saber el valor de F(b) y que conocemos las pendientes de las diferentes partes.
Podríamos calcular los valores de F(c), F(d) y F(b) usando la fórmula punto-pendiente para rectas (por ejemplo).
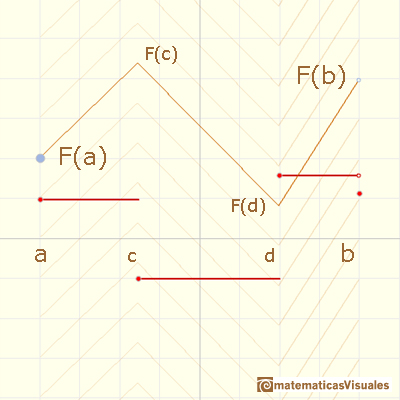
Si hay muchas piezas puede resultar costoso encontrar el calor de F(b).
F(x) es una función integral, entonces
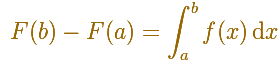
Este es el Teorema Fundamental del Cálculo aplicado a una situación particularmente sencilla.
Podemos calcular el área pieza a pieza para obtener la integral
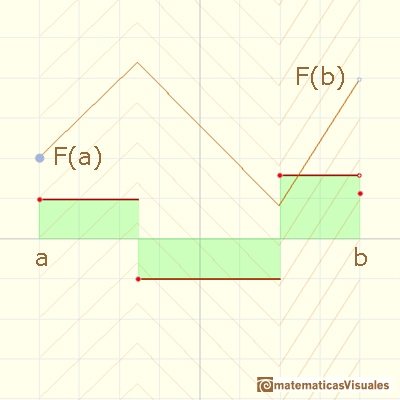
O podemos usar el valor intermendio y recordar que
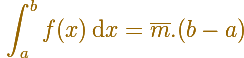
Ahora, esta fórmula relaciona el Teorema Fundamental del Cálculo con la fórmula punto-pendiente:
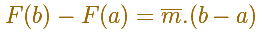
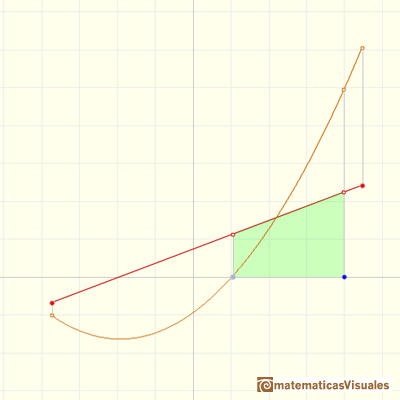
Ahora damos un paso más y vamos a integral funciones continuas lineales a trozos.
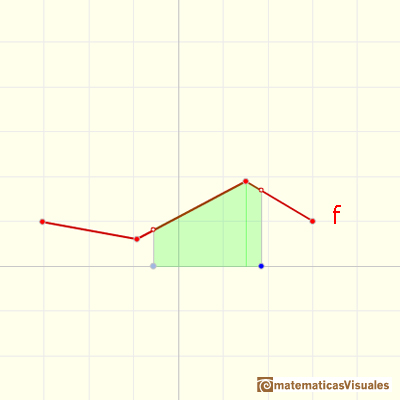
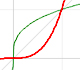
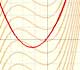
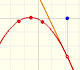
La función integral F(x) está formada por varias piezas de parábola conectadas.
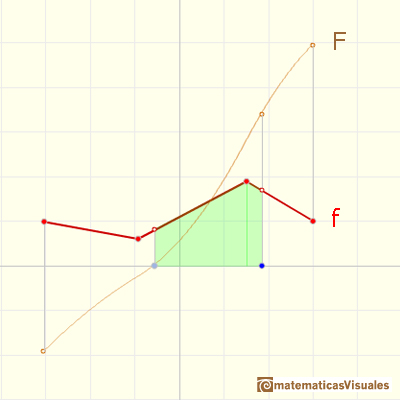
Apreciamos que la conexión entre las piezas de parábola es suave (esto es algo intuitivo, tendríamos que probarlo)
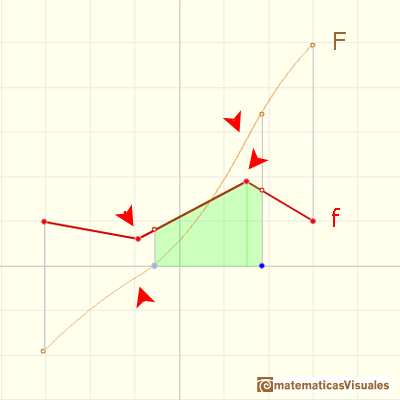
La función F(x) no es solo continua, también es diferenciable. Nos podemos convener un poco más de esta importante propiedad arrastrando el punto azul y moviendo la tangente. El cambio es suave. Esta es una propiedad general: cuando f es continua entonces F es más que continua, es diferenciable.
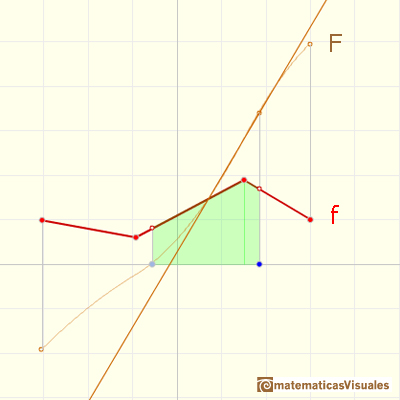
Si derivamos F obtenemos la función original f otra vez.
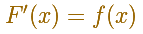
El valor medio de una función f(x) en un intervalo [a,b] viene dado por
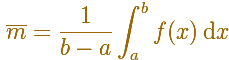
En el siguiente vídeo jugamos con este concepto.
Puesto que estas funciones son continuas, son un caso particular del Teorema del valor medio para integrales: Si f(x) es una función continua en un intervalo [a,b] entonces existe un valor c en [a,b] tal que
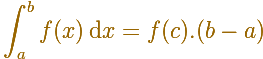
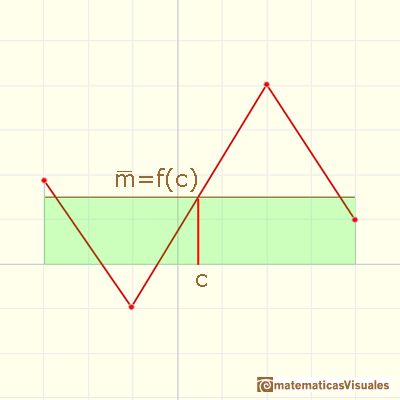
Un caso más general que podemos estudiar es el de las funciones lineales a trozos discontinuas.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES