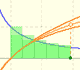
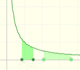
En su libro 'In pursuit of the Unknown', Ian Stewart resume en unas pocas líneas por qué esta ecuación es tan importante:
¿Qué nos dice?
Como multiplicar números haciendo una suma de números relacionados con los factores.
¿Por qué es tan importante?
Sumar es mucho más sencillo que multiplicar.
¿Para qué nos sirve?
Métodos eficientes para calcular fenómenos astronómicos como eclipses y orbitas planetarias.
Procedimientos rápidos para realizar cálculos científicos. La regla de cálculo, fiel compañera de los ingenieros.
Desintegración radioactiva y la psicofísica de la percepción humana.
(Ian Stewart, p. 22)
La necesidad de un procedimiento que facilitara operaciones largas como multiplicaciones, divisiones o raíces está
en el origen de la invención de los logaritmos por Napier.
C.H.Edwards Jr. escribió:
"El final del siglo XVI fue una época de cálculos numéricos ya que los desarrollos de la astronomía y la navegación
precisaban de una precisión cada vez mayor y más larga de los cálculos trigonométricos (...). La necesidad urgente de
algún dispositivo que acortara las laboriosas y tediosa multiplicaciones y divisiones con muchos decimales se resolvió
con la invención de los logaritmos por Napier y otros hacia el comienzo del siglo XVII." (pag. 142).
Las primeras tablas de logaritmos las publicó John Napier en 1614. Henry Briggs publicó en 1624 las primeras tablas de
logaritmos decimales (en base 10).
Ya sabemos que
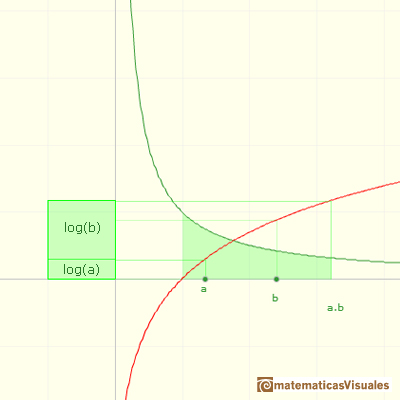
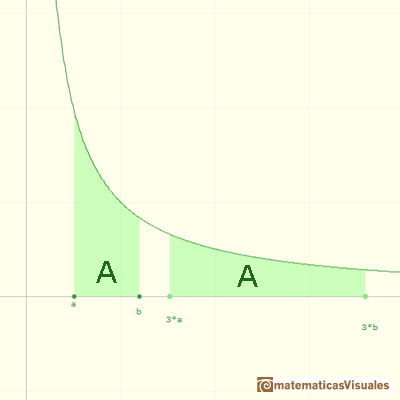
el logaritmo natural puede definirse como una integral de la hipérbola equilátera:
Usando una propiedad de la hipérbola podemos probar que:
Entonces es fácil probar la principal propiedad de los logaritmos:
[El camino utilizado para probar esta propiedad en estas páginas es visual e intuitivo.
Otro modo de probar esta propiedad es usando la regla de la cadena. Esta demostración la podemos ver en muchos libros, por ejemplo,
en el de Serge Lang. Después de hacer la demostración, Lang escribe: "¡Por favor, apreciemos la elegancia y eficacia del argumento", p. 177.
Por lo tanto, muy recomendable buscar esa otra demostración para ver otro punto de vista.]
REFERENCIAS
A. I. Markushevich, Areas and Logarithms, D.C. Heath and Company, 1963.
Serge Lang, A First Course in Calculus, Third Edition, Addison-Wesley Publishing Company.
Tom M. Apostol, Calculus, Second Edition, John Willey and Sons, Inc.
Michael Spivak, Calculus, Third Edition, Publish-or-Perish, Inc.
Otto Toeplitz, The Calculus, a genetic approach, The University of Chicago Press, 1963.
Kenneth A. Ross, Elementary Analysis: The Theory of Calculus, Springer-Verlag New York Inc., 1980.
C.H. Edwards, Jr., The Historical Development of the Calculus, Springer-Verlag New York Inc., 1979.
Ian Stewart, In pursuit of the Unknown, 17 Equations that changed the World, Basic Books, 2012.
MÁS ENLACES
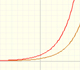
Estudiamos varias propiedades de las funciones exponenciales, sus derivadas y una introducción al número e.
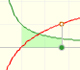
Integrando la hipérbola equilátera podemos definir una nueva función que es el logaritmo natural.

El número e, la base de los logaritmos naturales, se puede definir como una integral o como el límite de una sucesión relacionada con el interés compuesto. Ambas definiciones coinciden.
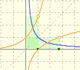
Partiendo de la definición de logaritmo podemos definir la exponencial como su inversa.

Diferentes hipérbolas permiten definir logaritmos y exponenciales (sus inversas).
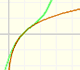
Mercator publicó su famosa serie para la función logaritmo en 1668. Euler descubrió una serie práctica para el cálculo.
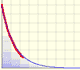
Las funciones exponenciales pueden modelar la desintegración radioactiva.

Al aumentar el grado del polinomio de Taylor se aproxima a la función exponencial en un intervalo más y más amplio.

La función exponencial compleja extiende la función exponencial real al plano complejo.

La función exponencial compleja es periodica. Su desarrollo de Taylor converge en todo el plano complejo.

El Teorema Fundamental del Cálculo afirma que toda función continua tiene una antiderivada y nos muestra cómo construir una usando la integral.

El Segundo Teorema Fundamental del Cálculo nos proporciona una herramienta muy potente para calcular integrales definidas (si conocemos una primitiva o antiderivada de la función).
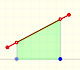
Como una introducción a las funciones lineales a trozos estudiamos el caso más sencillo, las funciones lineales restringidas a un intervalo abierto: sus gráficas son segmentos.
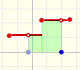
Una función constante a trozos (o función escalonada) está definida por varias subfunciones que son funciones constantes.
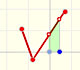
Una función continua lineal a trozos se define con varios segmentos o rayos que están unidos de un modo continuo, sin saltos entre ellos.
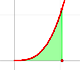
La integral de las funciones potencia era conocida por Cavalieri para n=1 hasta n=9. Fermat, entre otros, fue capaz de resolver este problema. Su técnica es un buen ejemplo del uso de progresiones geométricas.
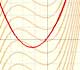
Si la derivada de F(x) es f(x) decimos que F es una antiderivada de f. También decimos que F es una primitiva o una integral indefinida de f.

La integral formaliza el concepto intuitivo de área. Para su definición aproximamos el área usando rectángulos.

Las funciones monótonas definidas en intervalos cerrados son interables. En estos casos podemos acotar el error que cometemos al aproximar la integral usando rectángulos.

Si consideramos el límite inferior de integración fijado y podemos calcular la integral definida para diferentes valores del límite superior de integración entonces podemos definir una nueva función: una integral indefinida de f.

Se trata de encontrar el polinomio de menor grado que pasa por una serie de puntos del plano. Es un problema de interpolación que aquí resolvemos usando los polinomios de Lagrange.

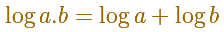
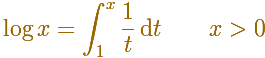
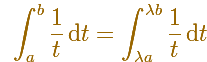
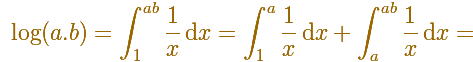
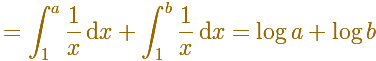
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR