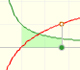
Desintegracion radioactiva
Podemos modelar la desintegración radioactiva usando una función exponencial.
El tiempo necesario para que el número de átomos radioactivos quede reducida a la mitad se llama periodo de semidesintegración.
Modificando los puntos cambiamos el número de átomos inicial y el periodo de semidesintegración.
Con los botones generamos el material radioactivo y controlamos el proceso de desintegración
Podemos oir la desintegración de los átomos con la opción "Sonido".
Si el número de átomos es muy grande, la razón entre el número de átomos desintegrados por unidad de tiempo y el número total de átomos es una magnitud constante que depende del tipo de átomo.
Podemos considerar que el hecho de que un átomo se desintegre es independiente de lo que les ocurra al resto. Tomando intervalos de tiempo pequeños, cada átomo se desintegra o no con una determinada probabilidad.
El número de átomos radioactivos que quedan se ajusta aproximadamente a una función exponencial.
REFERENCIAS
Zeldóvich y Yaglom - Matemáticas superiores. Ed. Mir. (p. 271)
 SIGUIENTE
SIGUIENTE
MÁS ENLACES
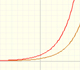
Estudiamos varias propiedades de las funciones exponenciales, sus derivadas y una introducción al número e.
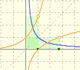
Hemos definido la función logaritmo como una integral de la hipérbola equilátera. Esta integral tiene una importante propiedad que nos permitirá usar los logaritmos para transformar multiplicaciones en sumas.
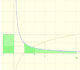
Usando los logaritmos podemos multiplicar dos números haciendo una suma: el logaritmo de un producto es igual a la suma de los logaritmos de los factores.
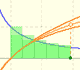
El número e se puede definir como áquel cuyo logaritmo es 1. Partiendo de esta definición podemos aproximar su valor.

El número e, la base de los logaritmos naturales, se puede definir como una integral o como el límite de una sucesión relacionada con el interés compuesto. Ambas definiciones coinciden.

Al aumentar el grado del polinomio de Taylor se aproxima a la función exponencial en un intervalo más y más amplio.

La función exponencial compleja es periodica. Su desarrollo de Taylor converge en todo el plano complejo.

El Teorema Fundamental del Cálculo afirma que toda función continua tiene una antiderivada y nos muestra cómo construir una usando la integral.

El Segundo Teorema Fundamental del Cálculo nos proporciona una herramienta muy potente para calcular integrales definidas (si conocemos una primitiva o antiderivada de la función).
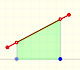
Como una introducción a las funciones lineales a trozos estudiamos el caso más sencillo, las funciones lineales restringidas a un intervalo abierto: sus gráficas son segmentos.
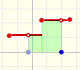
Una función constante a trozos (o función escalonada) está definida por varias subfunciones que son funciones constantes.
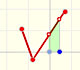
Una función continua lineal a trozos se define con varios segmentos o rayos que están unidos de un modo continuo, sin saltos entre ellos.
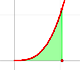
La integral de las funciones potencia era conocida por Cavalieri para n=1 hasta n=9. Fermat, entre otros, fue capaz de resolver este problema. Su técnica es un buen ejemplo del uso de progresiones geométricas.
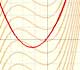
Si la derivada de F(x) es f(x) decimos que F es una antiderivada de f. También decimos que F es una primitiva o una integral indefinida de f.

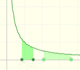
La integral formaliza el concepto intuitivo de área. Para su definición aproximamos el área usando rectángulos.

Las funciones monótonas definidas en intervalos cerrados son interables. En estos casos podemos acotar el error que cometemos al aproximar la integral usando rectángulos.

Si consideramos el límite inferior de integración fijado y podemos calcular la integral definida para diferentes valores del límite superior de integración entonces podemos definir una nueva función: una integral indefinida de f.













 ANTERIOR
ANTERIOR