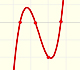
En esta página vamos a estudiar en mayor profundidad en comportamiento de las funciones racionales para valores grandes de |x| (x positivo o negativo). También empleamos la expresión 'cuando x tiende a infinito' (positivo o negativo).
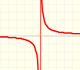
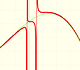
Ya hemos visto que cuando el grado del denominador es mayor que el grado del numerador (función racional propia) la función tiene una asíntota horizontal y=0 (el eje de las x o abcisas). Por ejemplo, ese es el caso de la hipérbola equilátera.
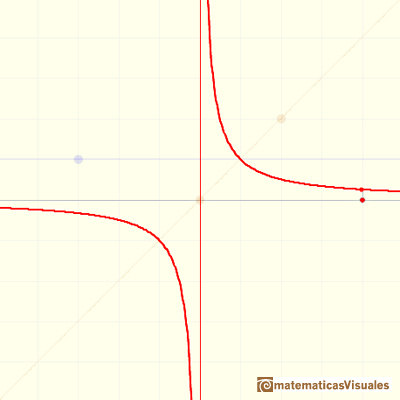
Si el grado del numerador es igual o mayor que el del denominador esta función racional es impropia. Podemos dividir el numerador entre el denominador y obtendremos un cociente y un resto. Este resto es un polinomio cuyo grado es menor que el del denominador. El resto dividido entre el denominador es una función racional propia y contribuye poco al valor de la función si consideramos valores grandes, en valor absoluto, de la variable x.
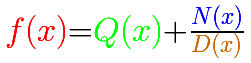
Ya hemos estudiado algún caso de función racional impropia pero solo cuando el grado del numerador es igual al del denominador. En estos casos, al dividir, obtenemos un cociente que es un número (un 'polinomio de grado 0'). Entonces podemos escribir la función racional original como un número más una función racional propia.
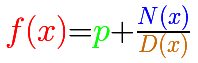
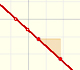
En estos casos la función tiene una asíntota horizontal. La podemos escribir con ese cociente que obtenemos al dividir. Esa asíntota es una recta horizontal, una función constante. Ese cociente es muy fácil de obtener pues basta con considera los términos de mayor grado del numerador y del denominador y dividirlos. Si una función racional tiene una asíntota, la gráfica de la función se acerca 'tanto como queramos' a esa recta al considerar valores arbitrariamente grandes de la variable x. También se acercará a la asíntota al considerar valores negativos grandes en valor absoluto.
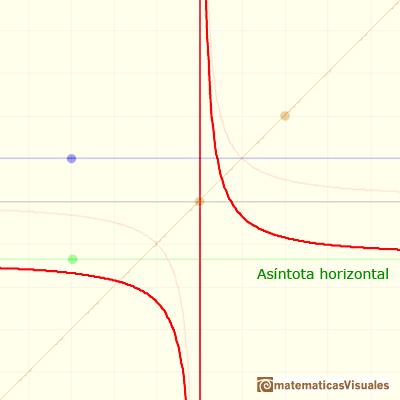
Esta es la ecuación de la asíntota horizontal:
Cuando el grado del numerador es mayor estrictamente que el grado del denominador no tenemos asíntota horizontal.
En esta página vamos a considerar el caso en el que el grado del numerador es 1 más el grado del denominador.
Como antes, podemos dividir numerador entre denominador y, usando el cociente y el resto, podemos escribir la función racional como un polinomio más una función racional propia. En estos casos, el cociente es un polinomio de grado 1. Esta linea recta controla el comportamiento de la función cuando el módulo de x es grande (lo que hace que la parte representada por la fracción propia contribuye muy poco al valor de la función).
El cociente Q(x) es lineal, es decir, Q(x)=ax+b, entonces y=ax+b es la ecuación de la asíntota de la función f(x).
Es decir, cuando el grado del numerador es exactamente uno más que el grado del denominador, el comportameinto de esta función racional cuando 'x tiende a infinito' es semejante a una función lineal oblicua. La gráfica de la función racional se aproxima a esta recta, tanto en valores extremos de x positivos como negativos. Esta recta es la asíntota oblicua de la función.
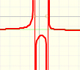
El caso más sencillo es cuando en numerador tiene grado 2 y el denominador es de grado 1:
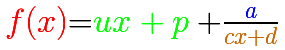
En este caso, esta es la ecuación de la asíntota oblicua:
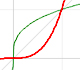
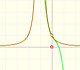
En el vídeo inicial podemos jugar con los tres elementos de este tipo de funciones racionales: un polinomio de grado 1 (en verde, una recta), el numerador (un número, en azul, una recta horizontal) y el denominador (otra recta en naranja).
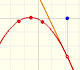
Por ejemplo:
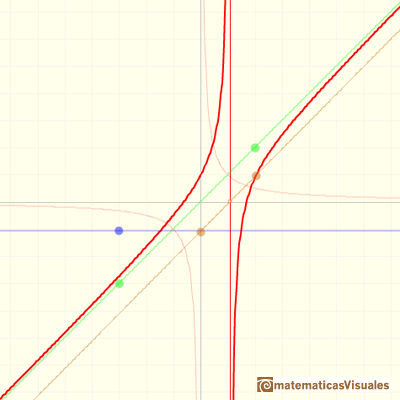
La fórmula de la gráfica anterior es:
Y esta es la ecuación de la asíntota oblicua en este caso:
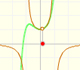
Otro ejemplo:
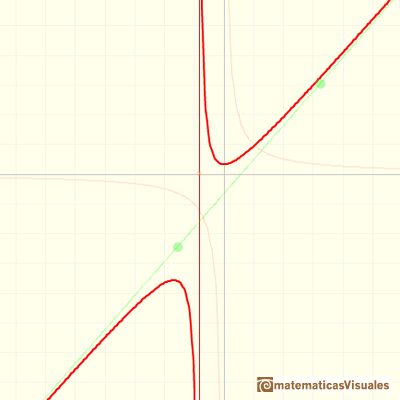
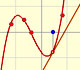
En el siguiente vídeo podemos ver funciones que tienen un polinomio de grado 3 en el numerador y un denominador de grado 2.
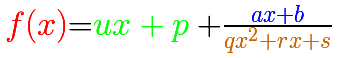
La ecuación del asíntota oblicua es:
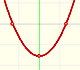
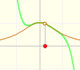
Los tres elementos de este tipo de funciones racionales son: Un polinomio de grado 1 (en verde, una recta), el numerador (en azul, otra recta) y el denominador (una parábola, en naranja):
Por ejemplo:
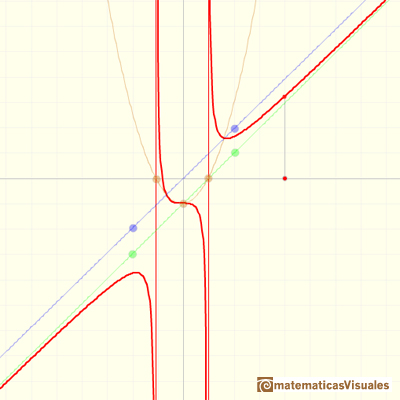
La fórmula para la gráfica anterior es:
La ecuación de la asíntota oblicua es:
Otro ejemplo:
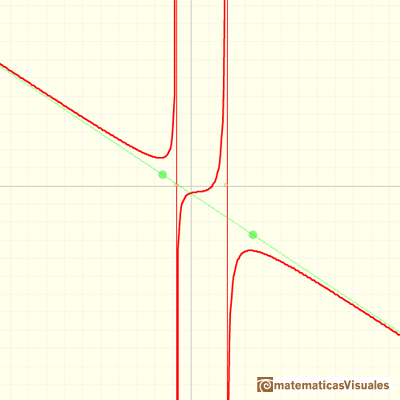
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES