Aquí tu solución....
En casa: Familia de funciones racionales (1)
Con esta página vamos a iniciar una serie en la que vamos a estudiar familias de funciones racionales dependiendo de un parámetro p.
Las funciones racionales extienden a las funciones polinómicas. En estas páginas estudiaremos el dominio, continuidad, asíntotas verticales y discontinuidades evitables de estas funciones.
Son un complemento a otras páginas que tratan el tema con muchas aplicaciones interactivas. El siguiente enlace sería una de ellas.
Las funciones racionales son las que pueden escribirse como cociente de dos polinomios. Las funciones racionales lineales son las más sencillas de este tipo.
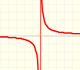
Recordamos que las funciones racionales se escriben como cociente de polinomios.
En esta serie vamos a considerar solamente polinomios de grado igual o menor que 2. Son las más sencillas pero ya nos muestran varios comportamientos interesantes que queremos estudiar.
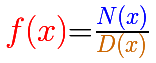
Fíjate que en la fórmula se usa un código de colores: el numerador está en azul y el denominador en marrón. La función racional en rojo.
Estos colores se usan también en los vídeos y son una ayuda importante para comprender estas funciones.
En la siguiente animación podemos ver cómo cambian las funciones racionales de una familia de funciones según varía el valor del parámetro p.
Tenemos que ver el vídeo y decidir la fórmula de esta familia de funciones:
a) En el nombre de la FUNCIÓN pondremos un subindice p para indicar que la familia depende de ese parámetro. Algo así:
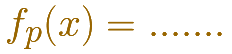
b) La segunda tarea consiste en determinar el DOMINIO de esas funciones. En algunas ocasiones ese dominio dependerá del parámetro p.
En otros casos el dominio es común para todas las funciones de la familia. ¿Ves el por qué?
c) Me preguntan por la CONTINUIDAD de las funciones de esta familia. Ahora ya podemos contestar la frase:
Las funciones de esta familia de funciones racionales que dependen del parámetro p son continuas en su dominio que es ....
Tendremos que especificar ese dominio, quizás dependiendo de p.
Es decir, si me preguntan por la continuidad debo contestar sobre la continuidad.
d) Después pasamos a tratar un asunto interesante que es el que nos ocupa en estas páginas: el comportamiento de la función para valores próximos a los valores de la variable que no están en el dominio de la función.
Ese es el estudio de las 'DISCONTINUIDADES de la función'.
En el caso de las funciones racionales este comportamiento puede ser de dos tipos:
1) Los valores de la función 'se hacen muy grandes', positivos o negativos, 'más grandes que cualquier cota o número que nos podamos imaginar'.
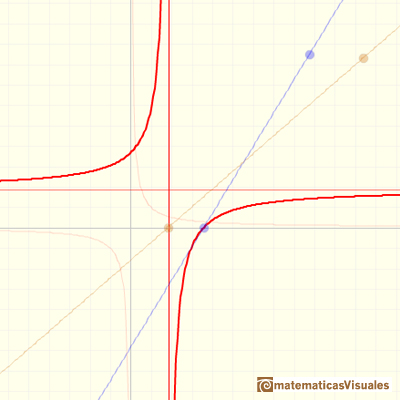
Decimos entonces que la función 'tiene' una ASÍNTOTA VERTICAL en en x=...
Como una notación, escribimos que la función 'se hace infinito' pero hay que especificar si es positivo o negativo.
En el caso de las funciones racionales, la asíntota lo es 'por la derecha' y 'por la izquierda', por ambos lados, pero ya sabemos que 'el infinito' puede ser en unos casos positivo y en otros negativo.
Usaremos los límites laterales para expresar este comportamiento.
2) Los valores de la función para valores de x, la variable independiente, próximos al valor que estamos estudiando se aproxima a un valor real concreto. En el caso de las funciones racionales esto lo hará 'por la derecha' y 'por la izquierda'.
El valor será el mismo. Es decir, los dos límites laterales existen, son números reales, y son iguales. Luego decimos que el límite existe y es igual a ese valor.
Cuando nos encontramos en esta situación no hace falta referirse a los límites laterales pues sabemos que el límite va a existir.
Notad que se trata de una indeterminación 0/0 que resolvemos descomponiendo los polinomios y simplificando.
Decimos que la función tiene 'un hueco'. Ese hueco es más que microscópico pero lo representamos con un circulito hueco.
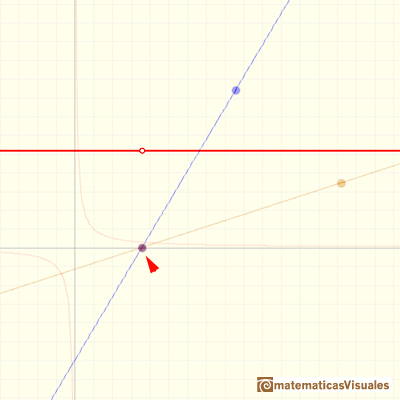
En estos casos hablamos de DISCONTINUIDAD EVITABLE.
Vamos a ver qué significa una DISCONTINUIDAD EVITABLE en el caso de las funciones racionales.
Cuando estudiamos Álgebra simplificamos expresiones de este tipo, sin problemas aparentes:
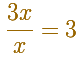
Cuando estudiamos Análisis pensamos en las funciones y entonces podemos escribir:
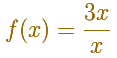
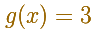
Si nos fijamos en estas funciones resulta que la primera es una función racional.
La segunda es una función polinómica (de grado 0). Es una función constante.
Si pensamos en sus dominios resulta que:
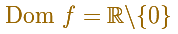
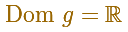
Luego las funciones son distintas pues tienen dominios distintos. Aunque se parecen mucho.
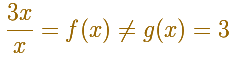
Decimos que la función g es una extensión de f.
Lo que hemos hecho son dos cosas:
1) Hemos extendido en dominio de la función f que ahora es todos los números reales.
2) Hemos asignado el valor 'adecuado' a f(0) de modo que la función es continua. 'Hemos tapado el hueco'.
Ese es el sentido de discontinuidad evitable: se extiende la función adecuadamente de modo que sea continua.
Fíjate también que hubiéramos podido extender la función f de otros modos. Por ejemplo, decir que f(0) = 7. Esta extensión no haría a la función f continua en el 0. En este caso tendríamos una DISCONTINUIDAD DE SALTO.
¿Te animas a resolver este ejercicio?
a) Determina la fórmula de la familia de funciones, justifica brevemente cómo has llegado a ella.
b) Dominio.
c) Continuidad.
d) Estudio de discontinuidades. Tipos.
Enviar una fotografía del ejercicio a mi contacto para su publicación.
Contacto para dudas, comentarios, enviar fotos con construcciones matemáticas o respuestas.
Puedes ser el primero en enviar una respuesta.
En el siguiente enlace nos plantearemos un nuevo ejemplo:
Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.
ANTERIOR
MÁS ENLACES
Página con enlaces de actividades matemáticas que podemos hacer en casa sencillas. Pensadas para alumnops de edad aproximada 9-13 años.
Página con enlaces de actividades matemáticas fáciles que podemos hacer en casa. Pensadas para alumnos de Educación Secundaria, edad aproximada 12-16 años.
Página con enlaces de actividades matemáticas que podemos hacer en casa un poco más complicadas. Pensadas para alumnos de Bachillerato o último año de Educación Secundaria. Edad aproximada, a partir de 15 años.
Ejercicios de cálculo mental en el que se practican algunas estructuras básicas con el propósito de mejorar la seguridad y autoconfianza.
Si tenemos impresora en casa podemos imprimir plantillas en cartulina (o papel) y hacer interesantes construcciones. Muchas son sencillas y puedes intentar hacerlas con reglas y compás. Aunque no puedas hacerlas, también puedes mirarlas pues de ellas sacaremos interesantes consecuencias matemáticas.
El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.
En casa se actualiza, por lo menos, 5 veces a la semana mientras dura el confinamiento. Aquí se puede ver la sucesión cronológica de las publicaciones.
Contacto para dudas, comentarios, enviar fotos con construcciones matemáticas o respuestas.
La representación gráfica de datos nos muestra los datos de un modo visual e intuitivo. Se muestran ejemplos en relación con el estudiio de las visitas al sitio matemátivasVisuales.