Séptima y última página de esta serie dedicada a estudiar familias de funciones racionales dependiendo de un parámetro p.
En la primera entrega se hacen comentarios extensos sobre cómo estudiar este tipo de familias de funciones.

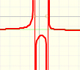
Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.
Estos son otros ejercicios de esta serie:

Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.

Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.

Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.

Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.

Representación de una familia de funciones racionales que dependen de un parámetro. Se estudia su dominio, continuidad, asíntotas verticales y discontinuidades evitables.
Son un complemento a otras páginas que tratan el tema con muchas aplicaciones interactivas. El siguiente enlace sería una de ellas.
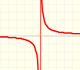
Las funciones racionales son las que pueden escribirse como cociente de dos polinomios. Las funciones racionales lineales son las más sencillas de este tipo.
Recordamos que las funciones racionales se escriben como cociente de polinomios.
Fíjate que en la fórmula se usa un código de colores: el numerador está en azul y el denominador en marrón. La función racional en rojo.
Estos colores se usan también en los vídeos y son una ayuda importante para comprender estas funciones.
En la siguiente animación podemos ver cómo cambian las funciones racionales de una familia de funciones según varía el valor del parámetro p.
Tenemos que ver el vídeo y decidir la fórmula de esta familia de funciones:
a) En el nombre de la FUNCIÓN pondremos un subindice p para indicar que la familia depende de ese parámetro. Algo así:
b) La segunda tarea consiste en determinar el DOMINIO de esas funciones. En algunas ocasiones ese dominio dependerá del parámetro p.
c) Me preguntan por la CONTINUIDAD de las funciones de esta familia.
d) El estudio de las 'DISCONTINUIDADES de la función': Asíntotas verticales y discontinuidades evitables, según los casos.
¿Te animas a resolver este ejercicio?
a) Determina la fórmula de la familia de funciones, justifica brevemente cómo has llegado a ella.
b) Dominio.
c) Continuidad.
d) Estudio de discontinuidades. Tipos.
Enviar una fotografía del ejercicio a
mi contacto para su publicación.
Contacto para dudas, comentarios, enviar fotos con construcciones matemáticas o respuestas.
MÁS ENLACES

Página con enlaces de actividades matemáticas que podemos hacer en casa sencillas. Pensadas para alumnops de edad aproximada 9-13 años.

Página con enlaces de actividades matemáticas fáciles que podemos hacer en casa. Pensadas para alumnos de Educación Secundaria, edad aproximada 12-16 años.

Página con enlaces de actividades matemáticas que podemos hacer en casa un poco más complicadas. Pensadas para alumnos de Bachillerato o último año de Educación Secundaria. Edad aproximada, a partir de 15 años.

Ejercicios de cálculo mental en el que se practican algunas estructuras básicas con el propósito de mejorar la seguridad y autoconfianza.

Si tenemos impresora en casa podemos imprimir plantillas en cartulina (o papel) y hacer interesantes construcciones. Muchas son sencillas y puedes intentar hacerlas con reglas y compás. Aunque no puedas hacerlas, también puedes mirarlas pues de ellas sacaremos interesantes consecuencias matemáticas.

El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.

En casa se actualiza, por lo menos, 5 veces a la semana mientras dura el confinamiento. Aquí se puede ver la sucesión cronológica de las publicaciones.

Contacto para dudas, comentarios, enviar fotos con construcciones matemáticas o respuestas.

La representación gráfica de datos nos muestra los datos de un modo visual e intuitivo. Se muestran ejemplos en relación con el estudiio de las visitas al sitio matemátivasVisuales.












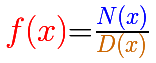
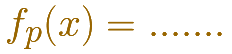
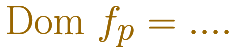

 ANTERIOR
ANTERIOR













