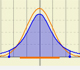
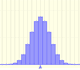
La distribución normal es un ejemplo importante referido a una variable aleatoria continua (la variable puede tomar cualquier valor real)
Podemos usar la distribución normal como una herramienta para calcular probabilidades. Por ejemplo, puede usarse para aproximar la distribución binomial (calcular probabilidades de la distribución binomial con números 'grandes' no ha sido tarea sencilla). Esta propiedad está en el origen de la curva normal.
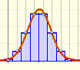
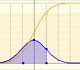
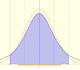
La función de densidad de una distribución normal tiene forma de campana. Es simétrica en torno a la media. El área total bajo la curva es 1 (como corresponde a una función de densidad).
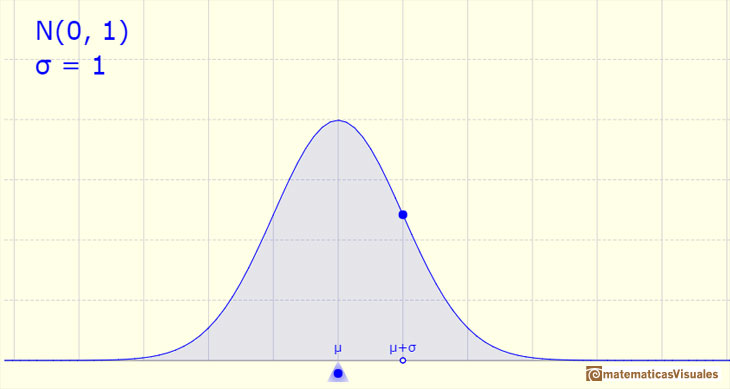
La densidad está concentrada en torno a la media y se hace muy pequeña conforme nos alejamos del centro por la derecha o la izquierda (las 'colas' de la distribución). Cuanto más alejado es el valor del centro de la función de densidad menos probable es observar ese valor.
Dos parámetros determinan una distribución normal: la media y la desviación estándar. Por tanto, puede ser adecuado hablar de las distribuciones normales, en plural, y decir que son una familia biparamétrica de distribuciones. Luego veremos que la más simple de ellas juega un papel destacado.

Si una variable aleatoria sigue una ditribución normal podemos escribirlo con esta notación:
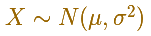
La media de la distribución determina el centro de la gráfica de la función de densidad.
Si cambiamos la media la forma de la gráfica no cambia, simplemente se traslada a derecha o izquierda.
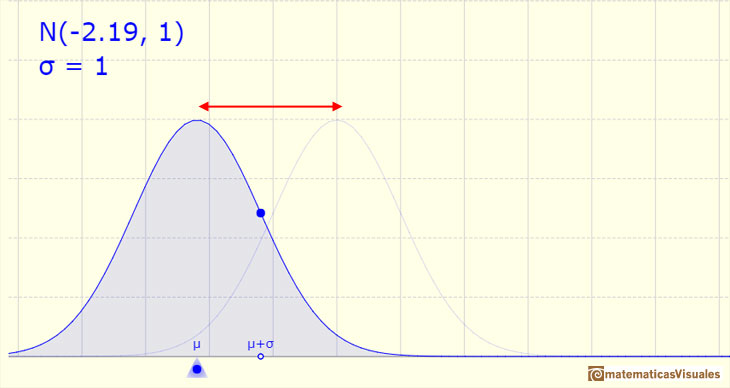
La función de densidad tiene dos puntos de inflexión que están localizados a una distancia de la media de una desviación típica (más y menos).
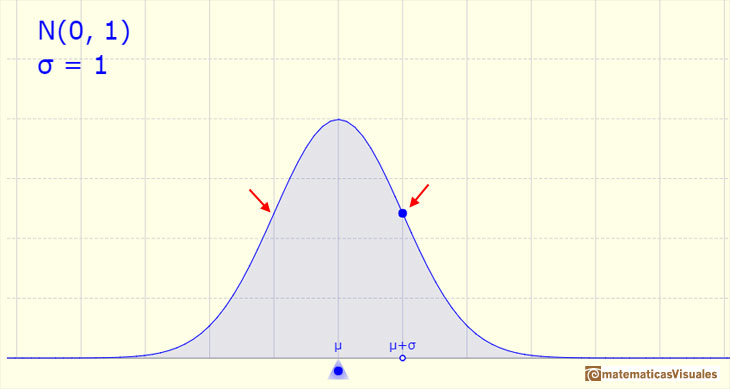
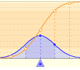
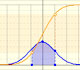
Aumentando la desviación estándar (si no modificamos la media, el centro de la gráfica no cambia) la forma de la curva cambia. La curva se hace más ancha y menos alta, es decir, la dispersión aumenta. Cuanto mayor es la desviación estándar mayor es la dispersión de la variable.
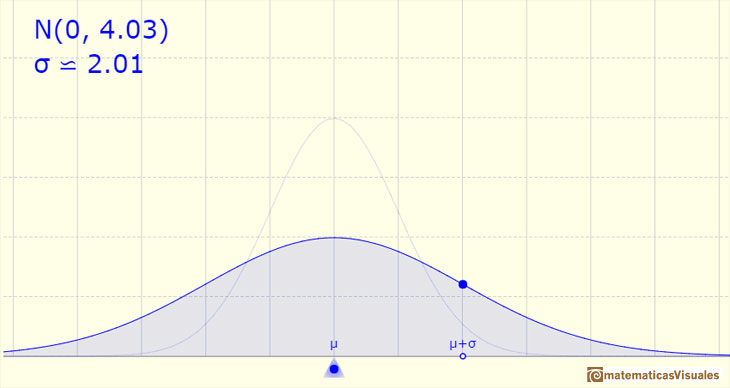
Si la desviación estándar es pequeña la curva es más alta y estrecha. La dispersión de la varible es menor.
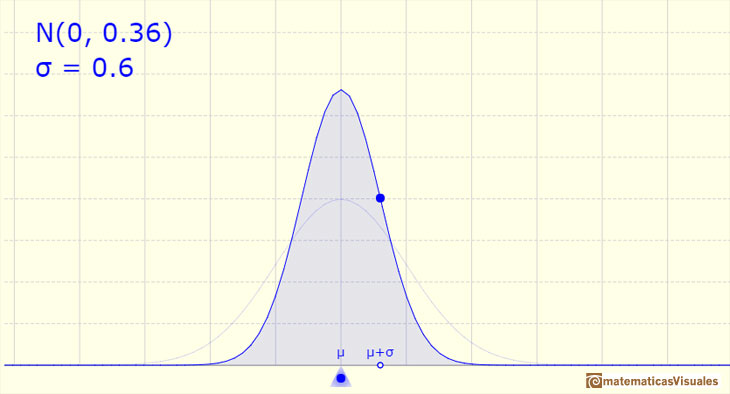
El ejemplo más sencillo es la llamada distribución normal estándar. Es el caso especial cuando la media es igual a 0 y la varianza es 1.
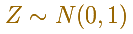
Juega un papel importante en los cálculos a través de un proceso que llamanos estandarización o tipificación de la variable.
La función de distribución (a veces se añade la palabra 'acumulada') tiene forma de S. A cada valor de x le corresponde la probabilidad de que la variable aleatoria X tome valores menores o iguales a x. A partir de la función de densidad (en nuestro caso, la 'campana'), para calcular los valores de la función de distribución se calcula el área bajo la curva desde menos infinito hasta x. Se trata de una integral que, en el caso de la distribución normal, sólo puede hacerse numéricamente.
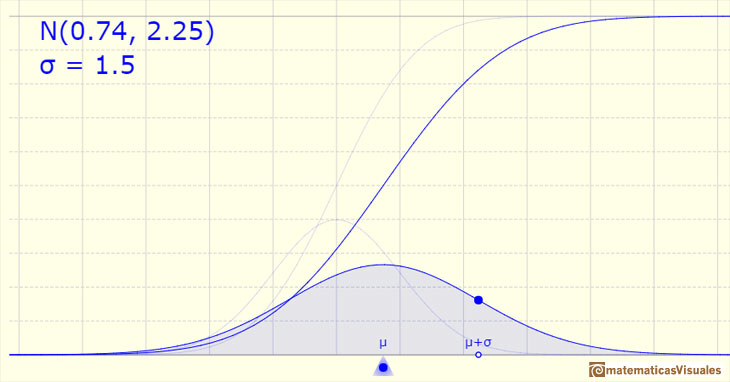
El caso particularmente importante es el de la distribución normal estándar. Usamos tablas y ordenadores para hacer estos cálculos. Una notación habitual para este caso de la función de distribución es:
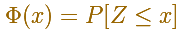
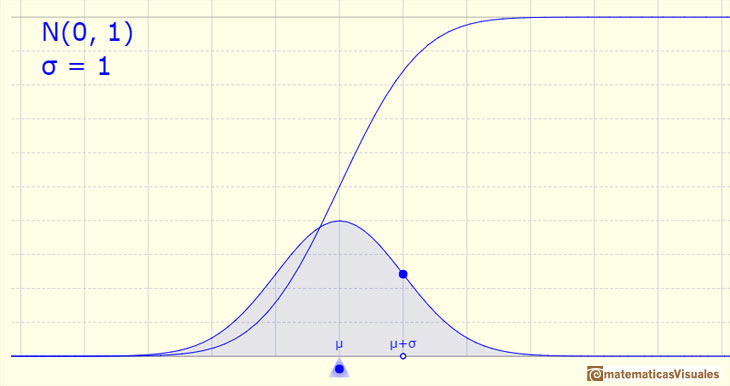
La media está representada por un triángulo y se puede interpretar como un punto de equilibrio. Al arrastrarlo se modifica también la media.
Arrastrando el punto sobre la curva (que es uno de los dos puntos de inflexión de la curva) se modifica la desviación típica.
Podemos ver la función de distribución acumulada y cómo cambia al modificar la media (simple traslación) y la desviación típica (reflejando la mayor o menor dispersión de la variable).
Los puntos rojos controlan la escala vertical y horizontal de la gráfica.
La distribución normal fue estudiada por Gauss (1809) en relación con la distribución de los errores en medidas astronómicas. Por este motivo se usa a veces el termino 'campana de Gauss' para referirnos a la función de densidad. Dos antecedentes importantes son de Moivre(1738) y Laplace (1774).
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES