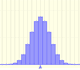
La distribución de Poisson es discreta (como la binomial) pues los valores que puede tomar la variable aleatoria son números naturales. Aunque en la distribución de Poisson los casos posibles en teoría son infinitos (numerable).
La distribución de Poisson se caracteriza por un solo parámetro landa.
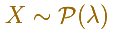
La función de densidad está definidad así:
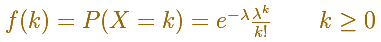
Su media es landa y su varianza también es landa:
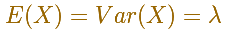
Pfeiffer and Schum escribieron en su libro "Introduction to Applied Probability":
"Encontramos esta distribución en situaciones en als que queremos contar el número de ocurrencias de un fenómeno en un intervalo de tiempo o espacio. Suponemos que se cumplen las siguientes condiciones:
(1) La probabilidad de que el fenómeno no ocurra en un intervalo de longitud 0 es 1.
(2) El número de ocurrencias en dos intervalos que no se solapan es independiente.
(3) La probabilidad de que se produzcan un número dado de ocurrencias en un intervalo depende de la longitud del intervalo pero no de su localización.
(4) Para intervalos pequeños, la probabilidad de que se produzca exactamente una ocurrencia se puede considerar proporcional a la longitud del intervalo.
(5) Para intervalos pequeños, la probabiliad de que se produzca más de una ocurrencia tiende a cero más rápido que la longitud del intervalo.
Se ha comprobado que estas asunciones son razonables en muchas situaciones diversas como:
1. Ciertos estudios de patrones de tráfico del número de coches que pasan por un determinado punto en un intervalo de tiempo de longitud t.
2. El número de llamadas de teléfono a una centralita en un intervalo de tiempo t.
3. El número de fallos de un sistema complicado en un intervalo de tiempo t.
4. El número de productos de un determinado tipo vendidos en un periodo de tiempo t.
5. El número de suicidios en un intervalo de tiempo t.
6. El número de bacterias en un determinado volumen t de líquido.
7. El número de accidentes laborales en un intervalo de tiempo t."
[Pfeiffer and Schum, pp. 198-200]
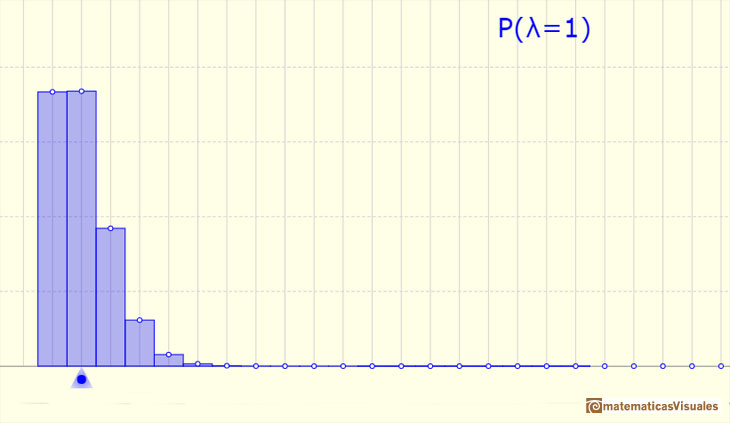
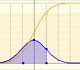
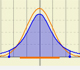
En ejemplo con mayor variabilidad:
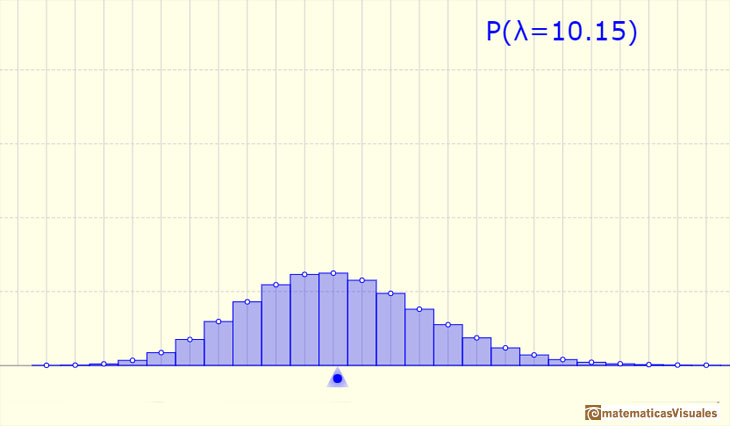
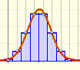
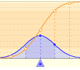
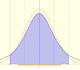
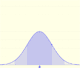
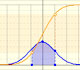
Podemos aproximar una distribución de Poisson con una distribución normal (que tenga la media y la varianza igual a landa). En este caso también podríamos usar una corrección de continuidad (como vemos en la aproximación normal a la distribución binomial).
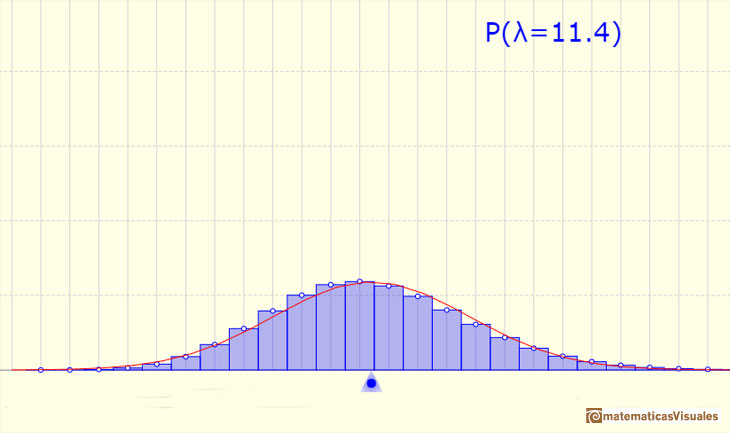
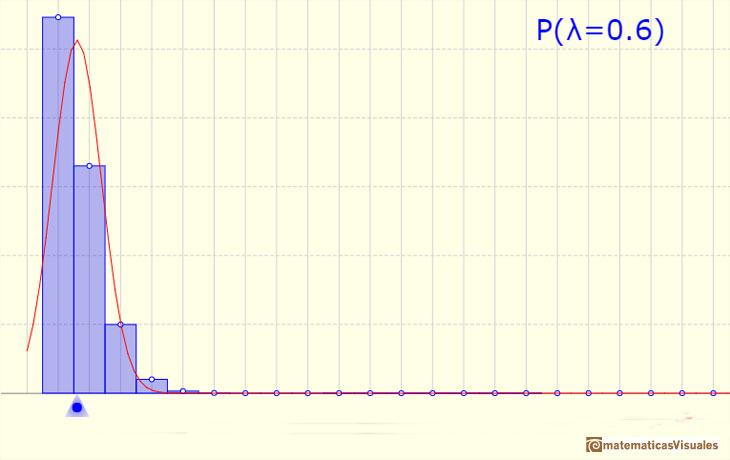
La media está representada por un triángulo azul que podemos ver como un punto de equilibrio. Arrastrando este triángulo modificamos el parámetro landa.
Podemos mostrar una curva normal que tiene la misma media y varianza que la distribución de Poisson correspondiente. Esta curva normal aproxima la distribución de Poisson en algunos casos.
Los puntos rojos controlan las escalas vertical y horizontal.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES