


Vamos a describir la construcción de un icosaedro que es un precioso sólido platónico.
Esta construcción del icosaedro se basa en que sus 12 vértices están en 3 rectángulos áureos.
Esta construcción es muy famosa. Muchos matemáticos la han recomendado para comprender este poliedro tan bonito
Por citar solo a tres diremos que aparece recomendada en libros de Félix Klein, David Hilbert y Coxeter. Y esto nos da una pista de lo interesante de esta construcción.

Recomiendo hacer este poliedro con madera contrachapada y una sierra de marquetería. Como se describe en la siguiente página:
Pero ahora muchos no tenemos estos materiales. Pero casi seguro que tenemos una caja de leche o de zumo.
La construcción resuslta sencilla pues solo necesitamos tres rectángulos.
Las cajas de leche se desarrollaron a partir de dos inventos fundamentales: la construcción de tetraedros a partir de tubos de cartón y la fabricación de un cartón flexible, resistente y apto para empaquetar alimentos. Ese cartón está formado por varias capas, siendo la más interior una capa plateada impermeable y muy resistente.
Con este material vamos a hacer nuestro icosaedro.
Abrimos una caja de leche y la limpiamos bien. La dejamo secar.
De esta caja tenemos que obtener 3 rectángulos áureos.

Para ello dibujaremos una plantilla con papel, cartulina o cartón de una caja de galletas.
El rectángulo que tenemos que dibujar es un rectágulo áureo. Lo hemos encontrado al hacer estrellitas que son pentágonos. La razón áurea es la razón entre la diagonal de un pentágono y su lado. Estudiaremos los rectángulos áureos en más ocasiones y aprenderemos a calcular el número áureo con exactitud. Ahora nos interesa la construcción.
El número áureo se puede aproximar así:
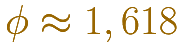
El ancho del rectángulo que podemos usar es de 5,2 cm.
Entonces el largo del rectángulo será:
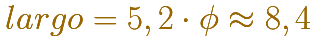
Dibujaremos el rectángulo sobre la plantilla. También los dos segmentos que dividen por la mitad el rectángulo a lo largo y a lo ancho.

Usaremos 7 agujas para marcar la plantilla sobre cada rectángulo de cartón. Fíjate que vamos a hacer un corte de 1 mm sobre uno de los largos y dejaremos 1 mm sin cortar sobre el corte que hacemos a lo largo por la mitad.

Cuando montemos los rectángulos esos dos cortes encajarán y darán mucha fuerza a nuestro modelo.
Usaremos un martillo u otra herramienta para clavar los alfileres. Hacerlo sobre una madera o montón de papeles para no estropear la mesa. Cuidado.
En cada rectángulo de cartón dibujaremos los cortes usando las marcas de los alfileres como referencia:

Cortaremos los tres rectángulos áureos:

Montaremos los rectángulos.

Este es el resultado:

Si tenemos unas gomitas elásticas de colores nos podemos plantear continuar la construcción.
ADVERTENCIA: La siguiente continuación sólo se recomienda a adultos hábiles. No a niños o chavales. Al clavar las agujas es muy fácil pincharse y hacerse daño. Sólo para personas hábiles y prudentes.
Aprovechando que el cartón tiene varias capas y que la plateada es muy resistente, se pueden clavar 12 alfileres en los vértices y unir los vértices con gomitas elásticas.

El resultado es muy bonito y es una especie de tensegridad debido a la flexibilidad del cartón. Solo cuando están todas las gomas colocadas la figura adopta su forma de icosaedro.
Irene, alumna de 2º ESO de Zaragoza, se atreve con las construcciones fáciles y las no tan fáciles. Aquí ha usado lana en vez de gomas para las aristas del icosaedro. Una buena solución, usando los materiales que tenemos en casa.


Pablo, alumno de 2º ESO de Zaragoza, no tenía lanas ni gomas y ha tenido una idea muy buena: ha cortado unas gomas de los dedos de un guante de goma. Excelente. De eso se trata, de usar los materiales que podemos encontrar.




 ANTERIOR
ANTERIOR
MÁS ENLACES













