 |
||
|
En casa: Continuidad de funciones definidas a trozos (2)
 En esta página vamos a estudiar la continuidad de una familia de funciones definidas a trozos dependiendo de un parámetro p. Se trata de un ejercicio muy parecido al anterior: 
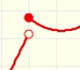
Estudio de la continuidad de una familia de funciones definidas a trozos que dependen de un parámetro. Las dos funciones que definen los trozos son afines.
Estas funciones son particularmente sencillas pues tienen dos trozos definidos usando funciones constantes, semirectas horizontales.
Lo primero es fijarse en el dominio de estas funciones En la siguiente animación podemos ver cómo cambian las funciones según varía el valor del parámetro p: Nos preguntan estudiar la continuidad de esta familia de funciones dependiendo del parámetro p. En estas circunstancias sencillas pero habituales en las que: - El dominio de la función está formado por todos los números reales. - Cada uno de los trozos es una función continua en un entorno abierto Sólamente se dan dos casos: 
Siendo a el valor de x para el que se 'unen' los dos subdominios correspondientes a los trozos de definición. Para completar el ejercicio nos falta concretar los valores de p para cada uno de esos casos. Es decir, tenemos que hacer una partición de los números reales en dos subconjuntos. Vemos que lo habitual es que esos dos subconjuntos sean muy diferentes en tamaño: uno estará compuesto por casi todos los números reales menos uno, dos o unos pocos. El otro suele ser el conjunto discreto complementario al que pertenecen solo uno, dos o unos pocos números. Una nota: si nos preguntan estudiar la continuidad de una función es más correcto contestar algo como 'la función ES continua en ...' que contestar algo como 'la función tiene una discontinuidad en ....' Ahora se trata de contestar a esta pregunta correctamente y con una buena argumentación. Destacaremos tres niveles de calidad de la respuesta: NIVEL -1 Nivel muy muy básico, sin dar ningún argumento. Miramos la animación y podemos imaginar que la respuesta correcta es: NIVEL 0 Aplico las tres pruebas o tests que tiene que pasar la función para el valor x=0. 
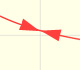
Estudio del concepto de continuidad de una función desde un punto de vista intuitivo. Algunos tipos de discontinuidades.
Pero en la prueba 2, la que es un poco más complicada, NO uso la terminología de límites y límites laterales. Pero hago unas cuentas que me dan la solución. NIVEL 1 Especificamos las tres pruebas y en la segunda uso el lenguage de los límites laterales. Compruebo que los límites laterales no coinciden y puedo afirmar que el límite planteado no existe en todos los casos, con alguna excepción. Concluimos, con un razonamiento correcto y completo, que:
La discontinuidad que se produce es una discontinuidad de salto. Una discontinuidad de salto se produce cuando existen los límites laterales (y, por lo tanto, son números reales) pero son distintos. ¿Te animas a resolver este problema? Envía una foto a mi contacto para su publicación. 
Contacto para dudas, comentarios, enviar fotos con construcciones matemáticas o respuestas.
Una respuesta, desde Alcalá de Henares En el siguiente enlace vamos a ver un caso sencillo semejante:
Estudio de la continuidad de una familia de funciones definidas a trozos que dependen de un parámetro. Discontinuides de salto. Las dos funciones que definen los trozos son afines.
MÁS ENLACES 
Página con enlaces de actividades matemáticas que podemos hacer en casa sencillas. Pensadas para alumnops de edad aproximada 9-13 años.
Página con enlaces de actividades matemáticas fáciles que podemos hacer en casa. Pensadas para alumnos de Educación Secundaria, edad aproximada 12-16 años.
Página con enlaces de actividades matemáticas que podemos hacer en casa un poco más complicadas. Pensadas para alumnos de Bachillerato o último año de Educación Secundaria. Edad aproximada, a partir de 15 años.
Ejercicios de cálculo mental en el que se practican algunas estructuras básicas con el propósito de mejorar la seguridad y autoconfianza.
Si tenemos impresora en casa podemos imprimir plantillas en cartulina (o papel) y hacer interesantes construcciones. Muchas son sencillas y puedes intentar hacerlas con reglas y compás. Aunque no puedas hacerlas, también puedes mirarlas pues de ellas sacaremos interesantes consecuencias matemáticas.
El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.
En casa se actualiza, por lo menos, 5 veces a la semana mientras dura el confinamiento. Aquí se puede ver la sucesión cronológica de las publicaciones.
Contacto para dudas, comentarios, enviar fotos con construcciones matemáticas o respuestas.
La representación gráfica de datos nos muestra los datos de un modo visual e intuitivo. Se muestran ejemplos en relación con el estudiio de las visitas al sitio matemátivasVisuales.
|
||
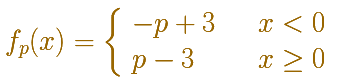
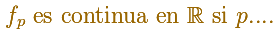
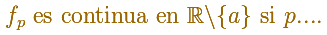
ANTERIOR