Ya hemos visto que no todos los rectángulos son semejantes.
Hay familias de rectángulos que tienen la misma forma. Una de esas familias está formada por los 'rectángulos raíz cuadrada de 2'.
Una manera de ver que dos rectángulos son semejantes es comprobar que colocados de determinada manera podemos decir que 'comparten una diagonal'.
En el vídeo utilizamos esa propiedad aplicada al caso de los rectángulos áureos.
En 'matemáticasVisuales En casa' hay tres páginas dedicadas a los rectángulos áureos que son un complemento a otras páginas dedicadas a estos rectángulos en este sitio web.
Estas tres páginas son una introducción muy sencilla a las propiedades de estos rectángulos.
Un rectángulo áureo es un rectángulo cuyos lados están relacionados con un pentágono regular.
El ancho del rectángulo es el lado de un pentágono. El largo del rectángulo áureo es como la diagonal de ese pentágono.
Al estudiar el pentágono ya hemos estudiado el rectángulo áureo.
Sabemos interesantes propiedades que ahora vamos a describir.
Y también sabemos dibujar un rectángulo áureo pues hemos aprendido a dibujar pentágonos. Hay otras maneras de hacerlo, puedes investigarlas y aprenderlas.
Queremos comparar el largo y el ancho del rectángulo. Un truquillo consiste en decir que una de estas dos medidas es 1. Con esto nos queda solo calcular la otra, que será la incógnita.
En nuestro caso usamos los números 1 para el ancho y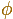 
para el largo,
que será nuestra incógnita.
La clave es partir del pentágono y llegar a esta proporción, a esta ecuación.
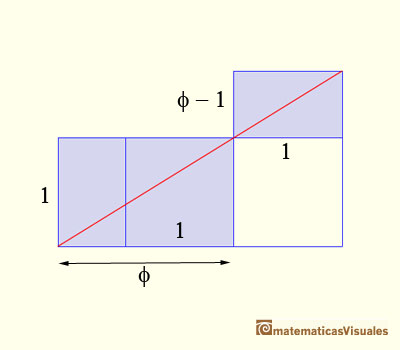
Esta ecuación nos dice cómo construir un rectángulo aúreo más pequeño a partir de un rectángulo áureo.
El miembro de la izquierda 'nos habla' del rectángulo grande: el numerador es su ancho y el denominador su largo, la base.
El miembro de la derecha relaciona el ancho y el largo de un rectángulo más pequeño. En el numerador está el ancho, que resulta de considerar el largo del rectángulo grande y quitarle su ancho (que es 1). En el denominador tenemos un 1 que es ahora el largo de este rectángulo más pequeño.
Es decir, que si a un rectángulo áureo le 'quitamos' un cuadrado lo que nos queda es otro rectángulo áúreo más pequeño.
Eso es lo que nos muestra el vídeo.
El ejercicio que se propone es dibujar un rectángulo áureo con regla y compás. Puedes usar la técnica del dibujo de la diagonal de un pentágono o explorar otros métodos que hay.
A partir de esta propiedad vamos a ver un ejemplo de un proceso infinito:
ANTERIOR
MÁS ENLACES
