Hemos visto que todos los cuadrados son semejantes. Tienen la misma forma.
También son semejantes, tienen la misma forma, todos los polígonos regulares con el mismo número de lados: los triángulos equiláteros, los cuadrados, los pentágonos regulares, etc.
Sin embargo, nos podemos imaginar que no todos los triángulos son semejantes, pues pueden tener formas muy distintas: unos son obtusángulos, otros acutángulos, etc.
Los triángulos los trataremos en otra ocasión pero es interesante notar que para que dos triángulos sean semejantes basta con que tenga sus ángulos iguales.
En el caso de los rectágulos nos podemos dar cuenta de dos cosas:
Primero, que todos los ángulos de todos los rectángulos son rectos.
Sin embargo, los rectángulos pueden tener formas muy diversas. No todos los rectángulos son semejantes entre sí.
Si nos fijamos en estos rectángulos, la tapa del libro y los tres rectángulos de cartulina, podemos ver que todos tienen distinta forma. No hay dos que sean semejantes.
Pero ahora nos fijamos en estos tres rectángulos, el amarillo, el naranja y el violeta. Tienen la misma forma.
Este sería un modo de comprobarlo que nos podría servir para empezar (un poco a ojo, para comprobarlo de verdad hay que hacer unas operaciones, una proporcionalidad).
Si trazamos la diagonal vemos que los tres rectángulos comparten una diagonal cuando están en esa posición (que podríamos llamar 'posición de Tales para los rectángulos').
Podemos decir que esos tres rectángulos forman una familia de rectángulos semejantes pues tienen la misma forma.
Hay varias familias de rectángulos semejantes que son especialmente interesantes.
En estas páginas de 'matemáticasVisuales En casa' trataremos de tres de esas famiias:
1) Los cuadrados que ya sabemos que son todos semejantes. (Los cuadrados son rectángulos y también son rombos).
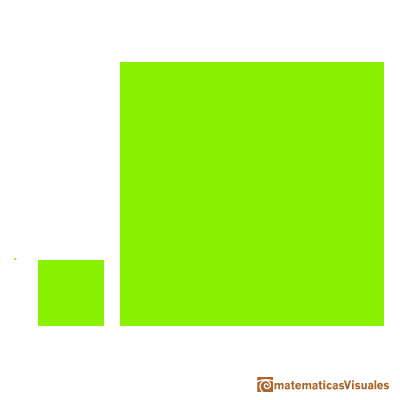
Cuando tenemos figuras semejantes pasa que si consideramos dos de sus medidas y las dividimos resulta siempre el mismo número, es una constante.
Por ejemplo, en el caso de los cuadrados podemos tomar la diagonal y un lado. Resulta que la división es constante.
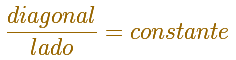
En el caso de los rectángulos en general es habitual considerar, para empezar, las dos medidas más sencillas que son el largo y el ancho. Entonces resultará que para todos los rectángulos de la misma familia se cumple:
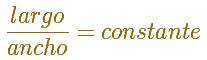
2) Los rectángulos que llamaremos 'rectángulos raíz cuadrada de 2'.
Estos rectángulos están muchas veces en nuestras manos pues las hojas de papel DinA4 son rectángulos de esta familia.
3) Los 'rectángulos áureos' que se forman con el lado y la diagonal de un pentágono regular y que tienen interesantes propiedades.
ANTERIOR
MÁS ENLACES
