


En esta página se han utilizado algunas aportaciones de Fernando de la Cueva, profesor del IES Clara Campoamor de Zaragoza y organizador del Taller del Talento Matemático de Zaragoza. Muchas gracias, Fernando.
Si cortamos un cubo con un plano podemos obtener diferentes secciones de ese cubo. Según el plano de sección obtenemos diferentes polígonos.
Queremos utilizar la técnica de construcción de poliedros con pajitas de refresco, un material que todos podemos conseguir.

En esta página se propone construir una sección rómbica de un cubo como la de la figura:


Se trata de una construcción sencilla que todos podemos hacer.
¿Te animas a hacer esta esta construcción? Si la haces, envía una foto a mi contacto. Me gustaría publicar alguna de estas fotos para animar a otros a construir. Gracias.
Después vamos a plantear algunos cálculos sobre esta construcción. Para hacerlos necesitaremos el teorema de Pitágoras y poco más.
Calcularemos el lado del rombo, las dos diagonales y su área. La construcción nos ayudará a hacerlo.

Veremos que en los resultados van a intervenir tres números irracionales especialmente interesantes.
Para hacer los cálculos vamos a utilizar los siguientes símbolos:
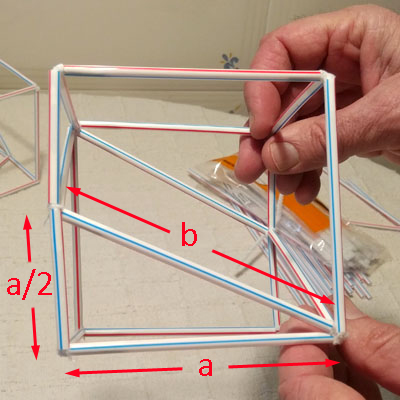
El dato del que partimos es la longitud de la arista del cubo a. Es nuestra 'variable independiente'. Esto quiere decir que nosotros podremos modificar su valor. La medida del lado de nuestro rombo b va a depender de a. Decimos que es la 'variable dependiente'.
Para nuestra construcción una persona usará una pajita de 10 cm, otro de 12,5 cm otro de 13 cm. Dependiendo de la longitud de la arista tenemos que corta los lados de nuestro rombo. En este caso, eso es lo que quiere decir 'variable independiente' (la que yo elijo, la arista del cubo) y 'variable dependiente', la que tengo que calcular.
Vamos a calcular la longitud del lado del rombo. Para eso usamos el teorema de Pitágoras:
Para indicar que b, el lado del rombo, depende de a, la arista del cubo, usamos la notación con paréntesis. Es la notación de FUNCIONES.
Podemos usar estas cuentas para cualquier caso particular. No tenemos que repetir las operaciones.
Por ejemplo, supongamos que nuestras pajitas, que son las aristas del cubo, miden 11 cm. Este va a ser nuestro caso particular (en cm):
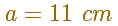
En un momento hacemos la cuenta (las unidades son cm):
Ahora vamos a ver las diagonales.
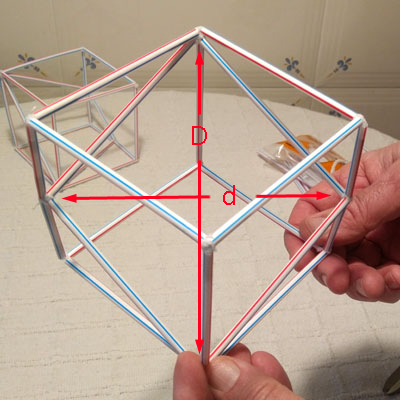
Si tienes la construcción delante verás que la diagonal pequeña del rombo es como la diagonal de una de las caras del cubo. Por lo tanto:
En nuestro caso particular (en cm):
La diagonal mayor del rombo es una diagonal interior del cubo. Esto se ve claramente si ves la construcción en realidad. Por eso hacer estas construcciones nos ayudan a comprender las propiedades geométricas de las figuras.
Para calcular la diagonal interior de un cubo (o de un paralelepípedo en general) se usa dos veces el teorema de Pitágoras.
En nuestro caso particular, la diagonal mayor del rombo mide (en cm):
Con estos datos podemos calcular el área del rombo.
Fíjate en una cosa importante: la arista del cubo está elevada al cuadrado. Esto ocurre cuando calculamos áreas. ¿Te imaginas lo que ocurre cuando calculamos volúmenes?
En nuestro caso particular, el área del rombo es:
Ahora las unidades son cm cuadrados.
La construcción y en nuestros cálculos han intervenido tres números irracionales interesantes:
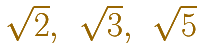
Estos números aparecen en muchas situaciones, por ejemplo:
En el cuadrado, en el triángulo equilátero, en el cubo, en la razón áurea y, por lo tanto, en el pentágono, el dodecaedro y el icosaedro.
Cuando aprendas a dibujar un pentágono regular a partir del lado con regla y compás verás que esta construcción está relacionada. Es importante.
Así es como lo ha construido Hugo, alumno de Fernando, usando papel de aluminio pues no ha podido conseguir limpiapipas.

Denis, alumno de 1º ESO, nos envía desde Alcalá de Henares esta construcción de la sección rómbica del cubo. Muy bien hecha, Denis.

David, alumno de 2º ESO, nos envía desde Zaragoza esta construcción de la sección rómbica del cubo. David ha usado unos alambres para unir las pajitas. Otra buena idea, a falta de limpiapipas.

 ANTERIOR
ANTERIOR
MÁS ENLACES













