La aproximación más intuitiva a la idea de semejanza de dos figuras es decir que 'tienen la misma forma'
Ya hemos visto que todos los cuadrados son semejantes, pues tienen la misma forma.
En general podemos decir que todos los polígonos regulares con un determinado número de lados son semejantes. Por ejemplo, todos los triángulos equiláteros son semejantes, todos los pentágonos regulares son semejantes,...
En cada familia de figuras semejantes podemos considerar dos medidas. Por ejemplo, en un cuadrado podemos considerar su diagonal y su lado. Si dividimos ambas medidas siempre obtenemos el mismo número, es una constante.
Esta es una propiedad muy importante que vamos a utilizar con la circunferencia.
Para empezar, estamos de acuerdo en que todas las circunferencias son semejantes, pues 'tienen la misma forma'.
Ahora vamos a considerar dos medidas de la circunferencia que van a ser la longitud de la circunferencia y su diámetro.
Entonces
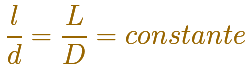
La división entre la longitud de una circunferencia y su diámetro es una constante muy importante. Para nombrarla usamos la letra griega 'pi'.
Esta es la definición de pi: pi es la división entre la longitud de una circunferencia y su diámetro.
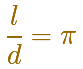
Solemos escribir la fórmula de la longitud de una circunferencia así:
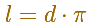
Pero la clave aquí es la definición del número pi y esta constante se basa en la noción de semejanza de las circunferencias.
Un detalle: cuando consideramos cuadrados hemos dividido la diagonal y el lado. Ambas medidas son segmentos. Al estudiar la circunferencia hemos considerado el diámetro pero también la longitud de la circunferencia. Esta segunda medida es la longitud de una curva. La noción de semejanza es útil cuando consideramos segmentos y también cuando consideramos curvas.
Veremos que la constante pi también interviene en el cálculo del área de un círculo:
ANTERIOR
MÁS ENLACES
