Hemos utiliado la técnica de construir poliedros usando pajitas de refresco y limpiapipas.

Construcción de los cinco sólidos platónicos con pajitas de refresco. Contamos sus elementos (sus caras, aristas y vértices) y vemos si son rígidos o no.
Al construir el cubo hemos visto que, con esta técnica, la supuesta fama de solidez del cubo no se cumple.
Para empezar, lo que ocurre es que el cuadrado no es rígido.
Si queremos hacer que el cuadrado sea rígido podemos añadirle una diagonal:

Podemos construir un cuadrado con pajitas de refresco. Notamos que no es rígido. Si lo deformamos obtenemos rombos. Para conseguir que sea rígido podemos añadir una pajita en la diagonal.
Esto nos da una idea para hacer rígido nuestro cubo. Vamos a añadir 6 diagonales de los cuadrados de sus caras.
Así los triángulos dan rigidez a las caras y a todo el poliedro.
Si se hace de un modo adecuado se obtiene un tetraedro.
En esta página se propone su construcción:
¿Cuáles son las medidas adecuadas de esta construcción?
Echa un vistazo a estos enlaces si no lo recuerdas:

Si colocamos una diagonal en nuestro cuadrado conseguimos darle rigidez. Calculamos la diagonal usando el teorema de Pitágoras.

Vamos a calcular la diagonal de un cuadrado. Para presentar la idea usaremos el lenguaje de las funciones.
Si quieres profundizar en esta construcción sigue el siguiente enlace:

Estudiamos algunas medidas de la construcción de un tetraedro en un cubo. Calculamos el volumen del cubo a partir de la arista del tetraedro.
Usaremos esta construcción para calcular el volumen de un tetraedro:
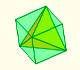
Podemos inscribir un tetraedro en un cubo. A partir de esta construcción calculamos el volumen de un tetraedro.
MÁS ENLACES

Página con enlaces de actividades matemáticas que podemos hacer en casa sencillas. Pensadas para alumnops de edad aproximada 9-13 años.

Página con enlaces de actividades matemáticas fáciles que podemos hacer en casa. Pensadas para alumnos de Educación Secundaria, edad aproximada 12-16 años.

Página con enlaces de actividades matemáticas que podemos hacer en casa un poco más complicadas. Pensadas para alumnos de Bachillerato o último año de Educación Secundaria. Edad aproximada, a partir de 15 años.

Ejercicios de cálculo mental en el que se practican algunas estructuras básicas con el propósito de mejorar la seguridad y autoconfianza.

Si tenemos impresora en casa podemos imprimir plantillas en cartulina (o papel) y hacer interesantes construcciones. Muchas son sencillas y puedes intentar hacerlas con reglas y compás. Aunque no puedas hacerlas, también puedes mirarlas pues de ellas sacaremos interesantes consecuencias matemáticas.

El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.

En casa se actualiza, por lo menos, 5 veces a la semana mientras dura el confinamiento. Aquí se puede ver la sucesión cronológica de las publicaciones.

Contacto para dudas, comentarios, enviar fotos con construcciones matemáticas o respuestas.

La representación gráfica de datos nos muestra los datos de un modo visual e intuitivo. Se muestran ejemplos en relación con el estudiio de las visitas al sitio matemátivasVisuales.











 ANTERIOR
ANTERIOR