La construcción de un cuadrado con pajitas nos ayudará a comprender que esa construcción no es rígida. También haremos
algunos cálculos sobre la relación entre el lado y la diagonal de un cuadrado.
Esa relación ya la hemos visto cuando hemos aprendido a doblar un cuadrado a partir de una hoja de papel.
Podemos construir un cuadrado doblando y cortando un folio. Se trata de un ejercicio muy básico de origami. Mediremos la diagonal.
Lo que estamos estudiando tiene relación con la idea de que todos los cuadrados 'tienen la misma forma', decimos que
todos los cuadrados son semejantes:
Todos los cuadrados son semejantes. Estudiamos la relación entre lado y diagonal de un modo intuitivo.
Construir un cuadrado con cuatro pajitas de la misma longitud es sencillo. Podemos unir los cuadrados con limpiapipas o
con papel de alumnio:
Veremos que el cuadrado así construido no es rígido. Se deforma con facilidad.
Al deformarse el cuadrado lo que obtenemos son rombos, es decir, cuadriláteros con sus cuatro lados iguales.
El cuadrado es un rombo especial, pues es un rombo rectángulo.
Si le añadimos una diagonal a un rombo conseguimos que sea rígido. En este caso no se trata de un cuadrado:
Pero, ¿qué tamaño tiene que tener la diagonal para que el rombo sea cuadrado?
Estas cuentas ya las hemos hecho antes:
Podemos construir un cuadrado con pajitas de refresco. Notamos que no es rígido. Si lo deformamos obtenemos rombos. Para conseguir que sea rígido podemos añadir una pajita en la diagonal.
Para ser exactos, el número es 'raíz cuadrada de 2'. Eso lo veremos aplicando el teorema de PItágoras en otra página.
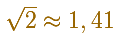
Si el lado de nuestro cuadrado, la longitud de esas 4 pajitas, es de 12 cm. ¿Cuánto medirá la diagonal?
También te puedes plantear construir el cuadrado más grande con su diagonal usando las pajitas que tengas.
Las mías miden 20 cm. Una de ellas será la diagonal. ¿Cuánto medirá el lado de ese cuadrado?
En el siguiente caso, ¿cuánto medirá el lado del cuadrado?
Resulta la mitad que antes.
Fíjate que si usas con la calculadora el valor 'raíz cuadrada de 2' el resultado es más preciso.
En el siguiente enlace repasamos la semejanza de cuadrados introduciendo el lenguaje de las funciones:
Todos los cuadrados son semejantes. Estudiamos la relación entre lado y diagonal usando el lenguaje de las funciones.
En esta página usamos el teorema de Pitágoras para calcular la diagonal de un cuadrado exactamente:
Si colocamos una diagonal en nuestro cuadrado conseguimos darle rigidez. Calculamos la diagonal usando el teorema de Pitágoras.
Aquí profundizamos un poco más en la relación entre diagonal y lado de un cuadrado:
Vamos a calcular la diagonal de un cuadrado. Para presentar la idea usaremos el lenguaje de las funciones.
MÁS ENLACES
Página con enlaces de actividades matemáticas que podemos hacer en casa sencillas. Pensadas para alumnops de edad aproximada 9-13 años.
Página con enlaces de actividades matemáticas fáciles que podemos hacer en casa. Pensadas para alumnos de Educación Secundaria, edad aproximada 12-16 años.
Página con enlaces de actividades matemáticas que podemos hacer en casa un poco más complicadas. Pensadas para alumnos de Bachillerato o último año de Educación Secundaria. Edad aproximada, a partir de 15 años.
Ejercicios de cálculo mental en el que se practican algunas estructuras básicas con el propósito de mejorar la seguridad y autoconfianza.
Si tenemos impresora en casa podemos imprimir plantillas en cartulina (o papel) y hacer interesantes construcciones. Muchas son sencillas y puedes intentar hacerlas con reglas y compás. Aunque no puedas hacerlas, también puedes mirarlas pues de ellas sacaremos interesantes consecuencias matemáticas.
El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.
En casa se actualiza, por lo menos, 5 veces a la semana mientras dura el confinamiento. Aquí se puede ver la sucesión cronológica de las publicaciones.
Contacto para dudas, comentarios, enviar fotos con construcciones matemáticas o respuestas.
La representación gráfica de datos nos muestra los datos de un modo visual e intuitivo. Se muestran ejemplos en relación con el estudiio de las visitas al sitio matemátivasVisuales.
ANTERIOR