


Hemos propuesto la construcción de un tetraedro inscrito en un cubo con pajitas de refresco.


Vamos a estudiar un poco esta construcción y calcular alguna de sus medidas.
Echa un vistazo a estos enlaces si piensas que te conviene repasar el caso del cuadrado:


Supongamos que la arista del cubo mide 1. ¿Cuánto mide la diagonal?
Fíjate que con esta notación el valor de la arista del cubo, que es 1, es lo que va dentro del paréntesis. Es nuestra 'variable independiente'. A la derecha del igual está el valor de la diagonal.
Si la arista mide 12,5 cm, ¿cuánto mide la diagonal?
El 12,5 puede 'salir fuera multiplicando'. Lo único que quiere decir es que la diagonal de un cuadrado de 12,5 cm de lado es 12,5 veces la diagonal de un cuadrado de lado 1.
Pero quizás sea mejor empezar por la diagonal, tomando la medida de nuestra pajita de refresco larga y cortar las aristas del cubo.
Supongamos que la diagonal mide 2. ¿Cuándo debe medir el lado del cuadrado?. Ahora buscamos el lado y el lado es lo que va dentro del paréntesis. El 2 es la diagonal y está a la derecha.
Ahora partimos de la diagonal que es de 20 cm. ¿Cuánto mide el lado del cuadrado?
¿Cómo podrías completar esta igualdad?
Es decir, la diagonal de un cuadrado de arista 1 es:
¿Cuánto mide el lado del cuadrado si queremos que la diagonal mida 1?
Ahora recordamos la fórmula del volumen de un cubo de arista a:
Ahora nuestro objetivo: Tenemos un tetraedro de arista 1, sabemos lo que mide l arista del cubo que lo contiene. Queremos escribir el volumen del cubo que contiene a un tetraedro de arista 1.
Este resultado lo vamos a utilizar para calcular el volumen de un tetraedro.
Como una interesante curiosidad vamos a pensar en girar nuestra construcción en torno a unos ejes.
Si hacemos que el tetraedro gire pero coincida consigo mismo resulta que el cubo también coincide.
Sin embargo, para algunos giros del cubo de modo que el cubo coincide con él mismo resulta que el tetraedro no coincide.
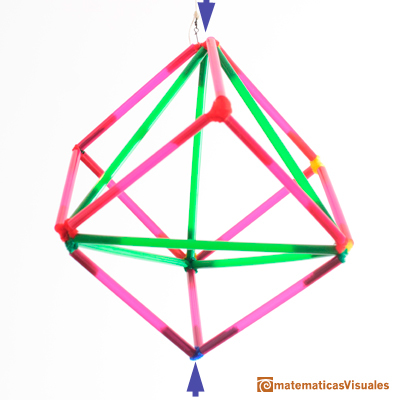
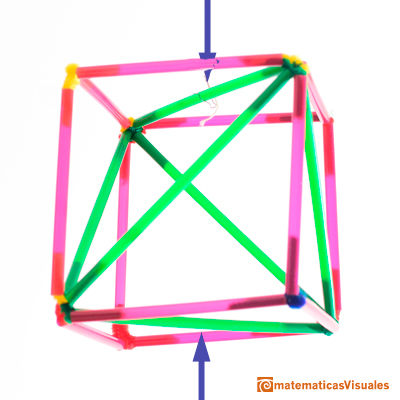
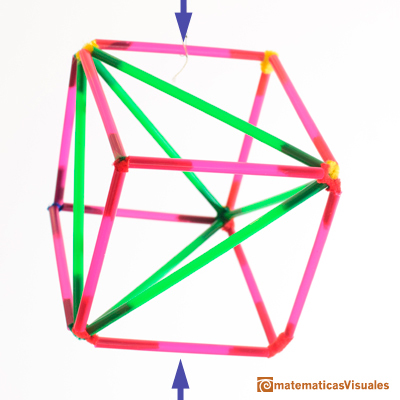
Este es un resultado importante y lo podemos ver simplemente girando nuestra figura.
Es conveniente fijarse que se puede inscribir dos tetraedros en un cubo.
Esta construcción es muy bonita. La combinación de dos tetraedros fue llamada por Kepler 'Stella octangula' o estrella de ocho puntas. La intersección de esos dos tetraedros es un octaedro.
El tetraedro es un poliedro dual de él mismo, o autodual. Cuando colocamos dos tetraedros de este modo decimos que están en posición recíproca.
La 'Stella octangula' es una estelación del octaedro. Se puede ver como un octaedro al que se ha añadido ocho tetraedros en sus caras.

 ANTERIOR
ANTERIOR
MÁS ENLACES












