Matematicas Visuales | The Complex Cosine Function: mapping an horizontal line

We already know that cos(z) is periodic with period .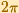

In this page we are going to explore how an horizontal line is transformed by the function cos(z), following Tristan Needham's Visual Complex Analysis.

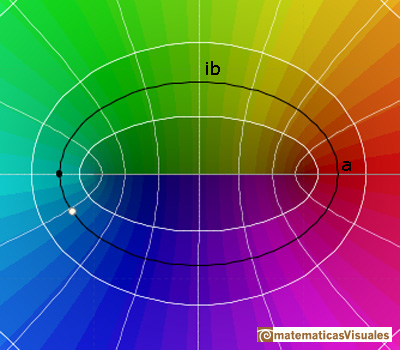
Playing the animation we can see that the image of

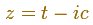
An horizontal line in the Complex Plane | matematicasvisuales

is "some kind of symmetrical oval" (is just the sum of two circular motions).

Cosine Complex Function | circular motions | matematicasvisuales

To calculate where this oval hits the real axis, we consider

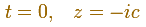
Point that is transformed in an imaginary value | matematicasvisuales

Then

The oval hits the real axis at this point:

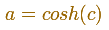
To calculate where this oval hits the imaginary axis, we consider

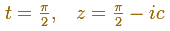
Point that is transformed in a real value

Then

The oval hits the imaginary axis at this point:

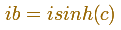
The oval is a perfect ellipse. If we calculate

Using

Considering the real and imaginary parts

We can write

Which is the familiar representation of the ellipse, that we can write (implicit formula):

To calculate the foci of the ellipse we can use

The shapes of the ellipse change as we vary c but all these ellipses are confocal.

The image under cos(z) of a vertical line is an hyperbola with the same foci as the ellipse. Ellipses and hyperbolas meet at right angles.

REFERENCES

Tristan Needham - Visual Complex Analysis. (pag. 88-89) - Oxford University Press

LINKS

The Complex Cosine Function

The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.

Taylor polynomials: Complex Cosine Function

The power series of the Cosine Function converges everywhere in the complex plane.

The Complex Exponential Function

The Complex Exponential Function extends the Real Exponential Function to the complex plane.

Taylor polynomials (2): Sine function

By increasing the degree, Taylor polynomial approximates the sine function more and more.

Inversion

Inversion is a plane transformation that transform straight lines and circles in straight lines and circles.

$Multifunctions: Powers with fractional exponent$

Multifunctions: Powers with fractional exponent

The usual definition of a function is restrictive. We may broaden the definition of a function to allow f(z) to have many differente values for a single value of z. In this case f is called a many-valued function or a multifunction.

More about complex functions

Examples of complex functions: polynomials, rationals and Moebius Transformations.