|
|
|
Equiangular Spiral through two points
We have already study the definition and several properties of equiangular spirals (or logarithmic spirals).
In an equiangular spiral the angle between the position vector and the tangent is constant.
Two transformations of an equiangular spiral with the same general efect.
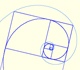
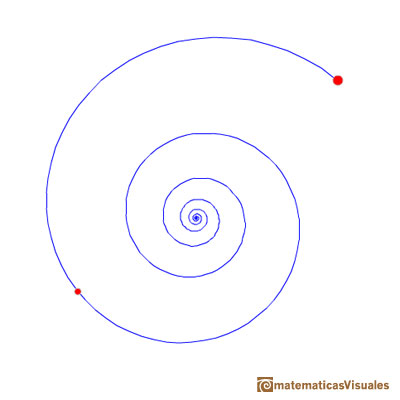
In this page we are going to see that there are infinitely many equiangular spirals through two points.
Some are anticlockwise:
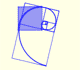
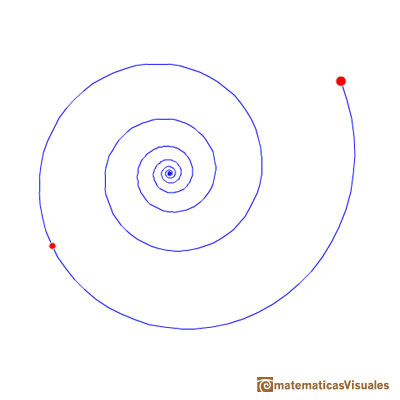
Or clockwise:
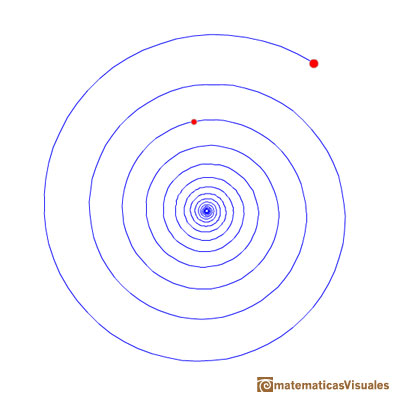
We can consider how many turns the spiral draw from one point to the other. In the next applet you can change how many rounds the spiral turns.
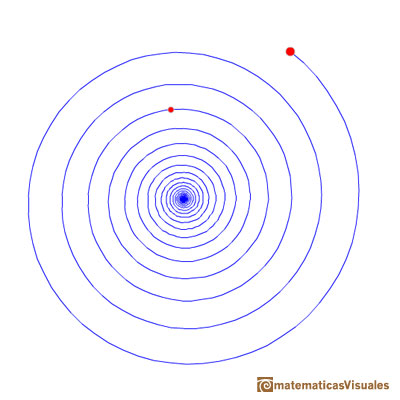
Equiangular spirals are connected with natural growth. Some examples of spirals:
You can play with this colorful spiral.
REFERENCES
Coxeter - Introduction to Geometry (John Whiley and sons)
Steinhaus - Mathematical Snapshots.
D'Arcy Thompson - On Growth and Form. (Cambridge University Press)
NEXT
A Dilative Rotation is a combination of a rotation an a dilatation from the same point.
PREVIOUS
Two transformations of an equiangular spiral with the same general efect.
MORE LINKS
In an equiangular spiral the angle between the position vector and the tangent is constant.
Two equiangular spirals contains all vertices of golden rectangles.
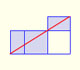
From Euclid's definition of the division of a segment into its extreme and mean ratio we introduce a property of golden rectangles and we deduce the equation and the value of the golden ratio.
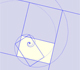
A golden rectangle is made of an square an another golden rectangle. These rectangles are related through an dilative rotation.
Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.
The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.
