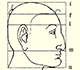
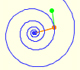
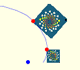
|
|
|
Drawing a Regular Pentagon with ruler and compass
If we start with a segment we can draw a regular pentagon, only using ruler and compass, that has this segment as one side.
We already know that the diagonal of a regular pentagon are in golden ratio to its sides and that the golden ratio is denoted by
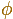and its value is:
This is the basic step:
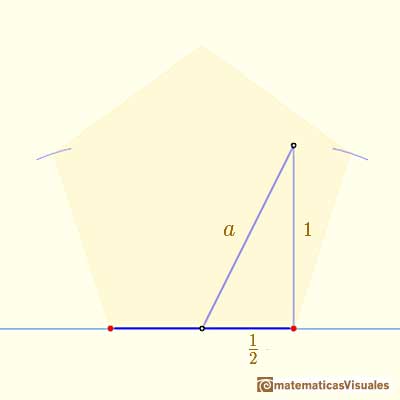
Then the value of a is:
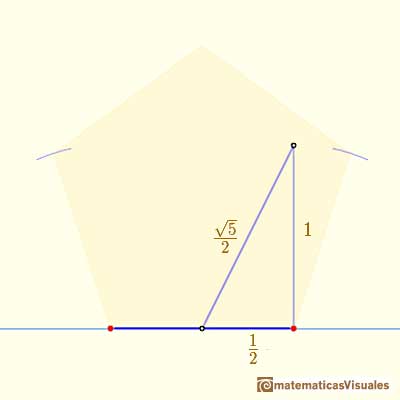
Then we can draw a segment with length the diagonal of the regular pentagon:
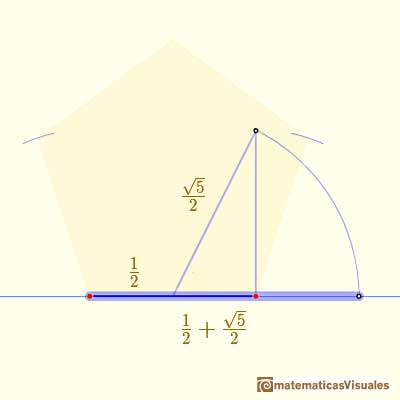
And we can finish our work and get a regular pentagon:
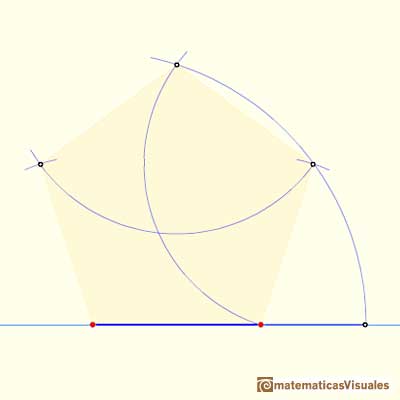
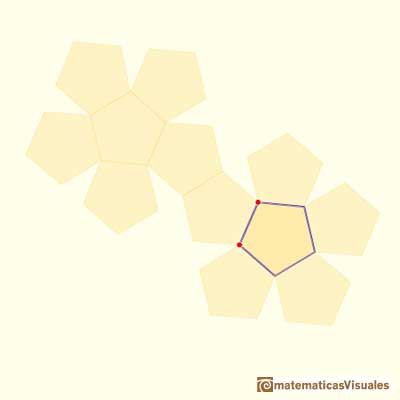
Drawing twelve pentagons we get the net of a dodecahedron:
NEXT
From Euclid's definition of the division of a segment into its extreme and mean ratio we introduce a property of golden rectangles and we deduce the equation and the value of the golden ratio.
PREVIOUS
The diagonal of a regular pentagon are in golden ratio to its sides and the point of intersection of two diagonals of a regular pentagon are said to divide each other in the golden ratio or 'in extreme and mean ratio'.
MORE LINKS
In his book 'Underweysung der Messung' Durer draw a non-regular pentagon with ruler and a fixed compass. It is a simple construction and a very good approximation of a regular pentagon.
A golden rectangle is made of an square an another golden rectangle. These rectangles are related through an dilative rotation.
Two equiangular spirals contains all vertices of golden rectangles.
The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron
With three golden rectangles you can build an icosahedron.
Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.
Durer was the first who published in german a method to draw ellipses as cone sections.
Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
Two transformations of an equiangular spiral with the same general efect.
In an equiangular spiral the angle between the position vector and the tangent is constant.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.
A Dilative Rotation is a combination of a rotation an a dilatation from the same point.