Maraldi Angle
The Maraldi angle is the obtuse angle of the rhombic face of a Rhombic Dodecahedron.
Giacomo Filippo Maraldi (1665-1729) was a French-italian astronomer and
mathematician. He calculate the angle that bears his name in 1712.
D'Arcy Thompson wrote:
"Kepler had deduced from the space-filling symmetry of
the honeycomb that its angles must be those of the rhombic dodecahedron:
and Swammerdam also recognised the same geometrical figure in the base
of the cell. But Kepler's discovery passed unnoticed, and Maraldi the
astronomer, Cassini's nephew, has the credit of ascertaining for the
first time the shape of the rhombus and of the solid angle which they
bound. [D'Arcy Thompson, p. ]
It is supposed that Maraldi took real measures of honeycombs but, in those
times it was impossible to get enough precision. Much more likely is
that Maraldi did a geometric reasoning.
We are going to study angles of the Rhombic Dodecahedron faces using basic Trigonometry.
Perhaps the easiest way to understand the Rhombic Dodecahedron is to see it as a cube with pyramids.
Adding six pyramids to a cube you can build new polyhedra with twenty four triangular faces. For specific pyramids you get a Rhombic Dodecahedron that has twelve rhombic faces.
We can put these six pyramids inside a cube.
A chain of six pyramids can be turned inwards to form a cube or turned outwards, placed over another cube to form the rhombic dodecahedron.
One important thing that we can understand only looking at this construction (it is highly recommended to build one) is that the angle between
two faces of the Rhombic Dodecahedron is 120º. Do you see why?.
Now we are going to study the rectangle that it is a section of the cube.
We start with the square. Remember that the diagonal of a square is:
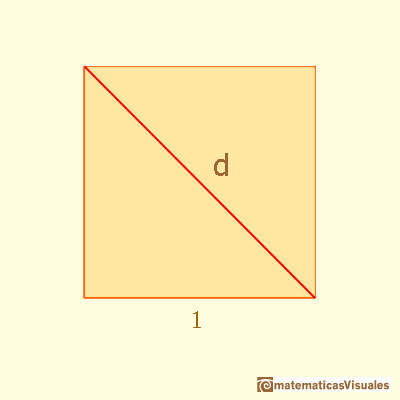
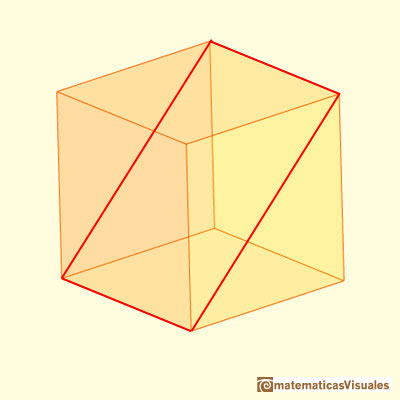
Then we can see our rectangle as a section of a cube. Sometimes this rectangle is called 'Silver Rectangle':
This rectangle is related with the standarized paper sizes used in Europe and other parts of the world.
There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.
One diagonal of this rectangle:
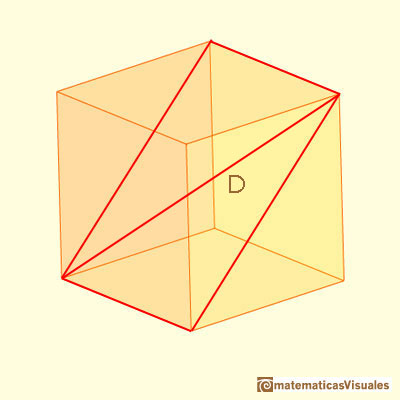
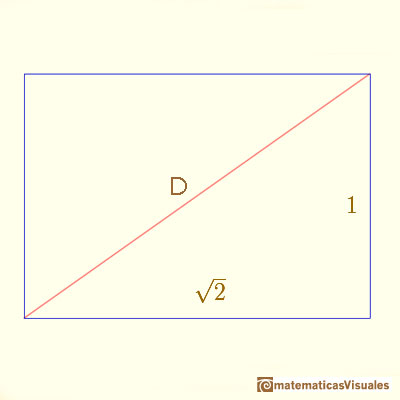
You can calculate D as a basic application of the Pythagorean Theorem:
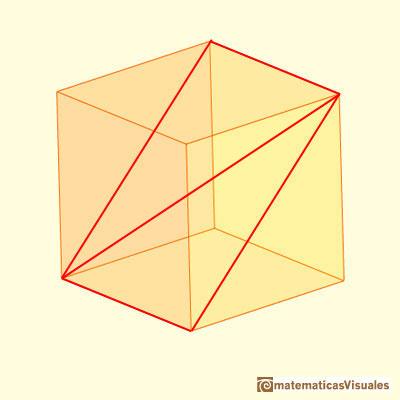
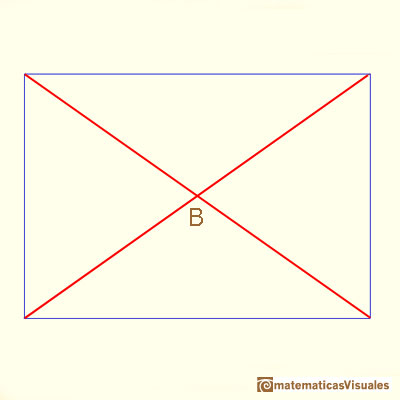
If we consider the two diagonals of this section, the point of intersection is the center of the cube:
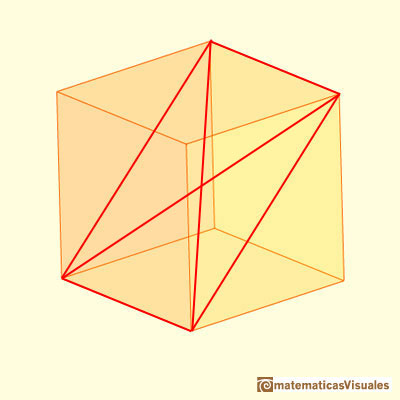
Now we are going to study the angles between the two diagonals (we need some basic knowledge about trigonometry):
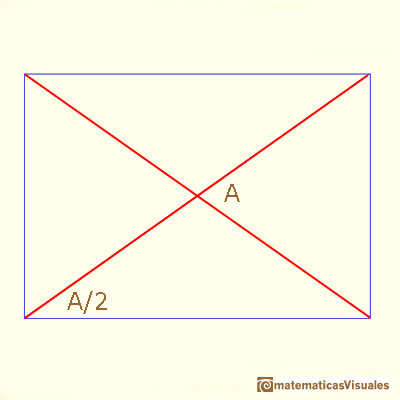
Maraldi angle is the obtuse angle B (the supplementary angle of A):
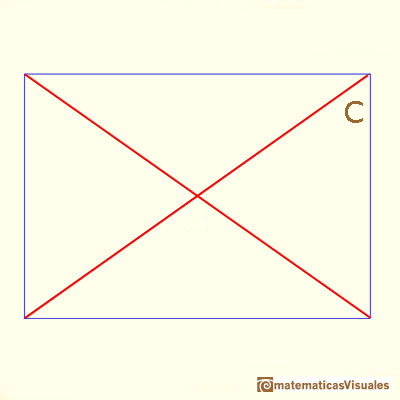
It is not difficult to calculate angle C:
Also
We are going to meet these two angles when we study the chamfered cube because our rectangle is related with this polyhedron.
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.
Another approach to find angle A:
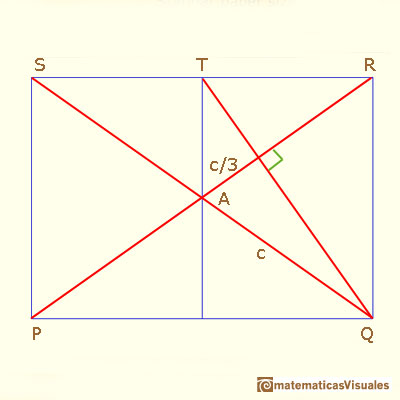
Can you explain it?
First, lines PR and QT are perpendicular because if we rotate 90 degrees counterclockwise the rectangle ....
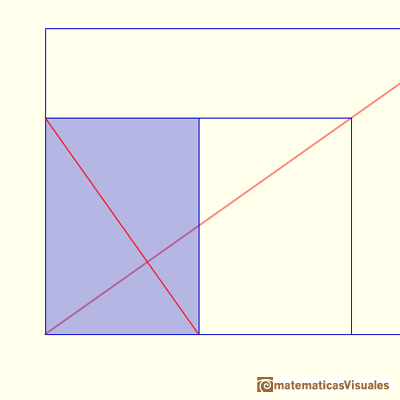
Second, lines PR and QT are two medians of triangle QRS, then the centroid divide ...
Now you can write cosA ...
After Maraldi, several mathematicians studied these angles, for example, Samuel Koening and Colin MacLaurin.
D'Arcy Thompson wrote:
When Colin Maclaurin studied the honeycomb in Edinburgh, a few years after
Maraldi in Paris, he proceeded to solve the problem without using
'any higher Geometry than vas known to the Antients' and he began his
account by saying: 'These bases are formed from Three equal Rhombus's, the
obtuse angles of which are found to be the doubles of an Angle that often
offers itself to mathematicians in Questions relating to Maxima and Minima'.
It was an angle of 109º 28' 16'', with its supplement of 70º 31' 44''.
And this angle of the bee's cell determined by Maraldi, Koening and Maclaurin
in their several ways, this angle which has for its cosine -1/3 and is
double of the angle which has for its tangent the square root of 2, is
on the one hand an angle of the rhombic dodecahedron, and on the other is
that very angle of simple tetrahedral symmetry which the soap-films within
the tetrahedral cage spontaneously assume, and whose frequent appearance and
wide importance we have already touched upon. [D'Arcy Thompson, p. 530]
We want to close a hexagonal prism as bees do, using three rhombi. Then, which is the shape of these three rhombi that closes the prism with the minimum surface area?.
This angle it is sometimes called the 'tetrahedral angle' because it is
the angle between two lines from the centroid of a regular tetrahedron
to two vertices. It has an important role in Chemistry.
REFERENCES
Johannes Kepler, 'The Six Cornered Snowflake: a New Year's gif' - Paul Dry Books, Philadelphia, Pennsylvania, 2010. English translation of Kepler's book 'De Nive Sexangula'.
With notes by Owen Gingerich and Guillermo Bleichmar and illustrations by the spanish mathematician Capi Corrales Rodrigáñez.
Colin Maclaurin, 'On the Bases of the Cells wherein the Bees deposite their Honey', 1743.
D'Arcy Thompson, 'On Growth And Form' - Cambridge University Press, 1942.
L. Fejes Tóth, 'What the bees know and what they do not know', Bull. Amer. Math. Soc. 70 (1964),
Hugo Steinhaus, 'Mathematical Snapshots' - Oxford University Press - Third Edition.
Magnus Wenninger, 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell, 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter, 'Matematical Recreations & Essays', The MacMillan Company, 1947.
NEXT
We want to close a hexagonal prism as bees do, using three rhombi. Then, which is the shape of these three rhombi that closes the prism with the minimum surface area?.
PREVIOUS
Humankind has always been fascinated by how bees build their honeycombs. Kepler related honeycombs with a polyhedron called Rhombic Dodecahedron.
MORE LINKS
The Rhombic Dodecahedron fills the space without gaps.
There are two essential different ways to pack spheres in an optimal disposition. One is related with the Rhombic Dodecaedron and the other to a polyhedron called Trapezo-rombic dodecahedron..
Using a basic knowledge about the Rhombic Dodecahedron, it is easy to calculate the density of the optimal packing of spheres.
Adding six pyramids to a cube you can build new polyhedra with twenty four triangular faces. For specific pyramids you get a Rhombic Dodecahedron that has twelve rhombic faces.
You can build a Rhombic Dodecahedron adding six pyramids to a cube. This fact has several interesting consequences.
Tetraxis is a wonderful puzzle designed by Jane and John Kostick. We study some properties of this puzzle and its relations with the rhombic dodecahedron. We can build this puzzle using cardboard and magnets or using a 3D printer.
There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.
Material for a session about polyhedra (Zaragoza, 9th May 2014). Simple techniques to build polyhedra like the tetrahedron, octahedron, the cuboctahedron and the rhombic dodecahedron. We can build a box that is a rhombic dodecahedron.
A Cube can be inscribed in a Dodecahedron. A Dodecahedron can be seen as a cube with six 'roofs'. You can fold a dodecahedron into a cube.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.
The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.
If you fold the six roofs of a regular dodecahedron into a cube there is an empty space. This space can be filled with an irregular dodecahedron composed of identical irregular pentagons (a kind of pyritohedron).
