|
|
|
Cuboctahedron (adapted from Leonardo da Vinci)
This video is an adaptation of the drawing that Leonardo da Vinci made of the cuboctahedron (exacedron abscisus vacuus) for Luca Pacioli's book 'De Divina Proportione'.
Pacioli wrote about the cuboctahedron (Spanish translation):
"El hexaedro despuntado o absciso plano, igualmente sólido o hueco, tiene veinticuatro líneas que originan en él cuarenta y ocho
ángulos superficiales, veinticuatro de los cuales son rectos y los demás agudos; tiene doce ángulos sólidos y está contenido por
catorce superficies o bases, seis de las cuales son cuadradas y ocho triangulares. Todas las mencionadas líneas son comunes a las
bases cuadradas y a las triangulares, porque las seis cuadradas unidas entre sí angularmente forman, necesariamente, ocho triángulos,
como hacían los hexágonos en el tetraedro absciso. Y este cuerpo se origina del cubo mediante el corte uniforme en la mitad de sus
lados, como demuestra de modo evidente su propia forma material."
('La divina proporción' de Luca Pacioli, page 91, Spanish translation by Juan Calatrava, Editorial Akal, 4th edition, 2008)
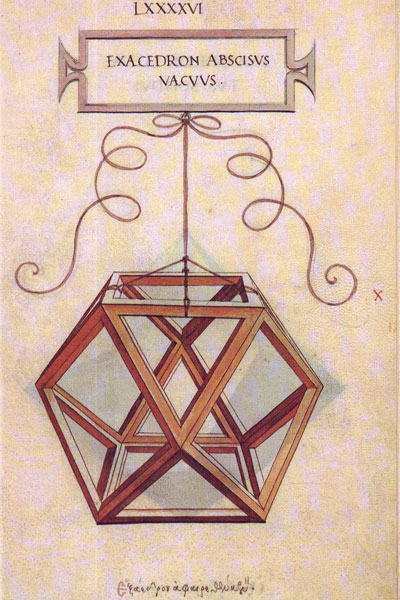
Leonardo da Vinci's drawing of the cuboctahedron (exacedron abscisus vacuus) for Luca Pacioli's book 'De divina proportione'. (There is an Spanish version, 'La divina proporción' Editorial Akal. Image used with permission of Editorial Akal).
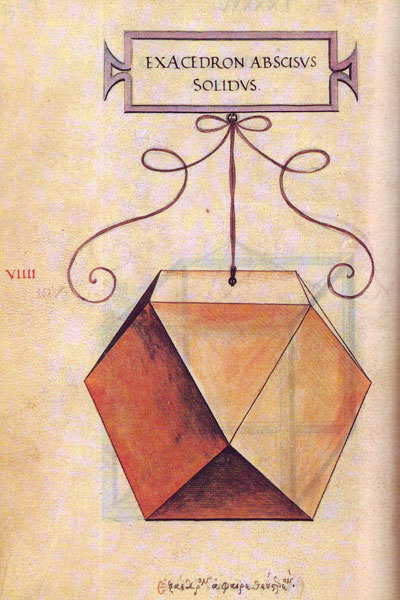
Leonardo da Vinci's drawing of the cuboctahedron (exacedron abscisus solidus) for Luca Pacioli's book 'De divina proportione'. (There is an Spanish version, 'La divina proporción' Editorial Akal. Image used with permission of Editorial Akal).
If you play with the interactive application you can get images like these:
REFERENCES
Luca Pacioli - La divina proporción - Ediciones Akal, 4th edition, 2004. Spanish edition of 'De divina proportione'. Translation by Juan Calatrava.
Leonardo da Vinci's Geometric Sketches Frank J. Swetz's article in MathDl, Loci:Convergence.
Leonardo da Vinci's Polyhedra George Hart's excellent website about polyhedra.
NEXT
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).
PREVIOUS
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.
MORE LINKS
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated tetrahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the octahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the rhombicuboctahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the Campanus' sphere.
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.
The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.
One eighth of a regular dodecahedon of edge 2 has the same volume as a dodecahedron of edge 1.
The volume of a tetrahedron is one third of the prism that contains it.
The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
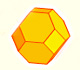
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.
These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.
The truncated tetrahedron is an Archimedean solid made by 4 triangles and 4 hexagons.
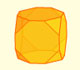
When you truncate a cube you get a truncated cube and a cuboctahedron. If you truncate an octahedron you get a truncated octahedron and a cuboctahedron.
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.