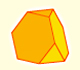
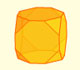
Rombicuboctahedron (adapted from Leonardo da Vinci)
This video is an adaptation of the drawing that Leonardo da Vinci made of the rhombicuboctahedron or small rhombicuboctahedron (Vigintisex basium planus vacuus) for Luca Pacioli's book 'De Divina Proportione'.
Pacioli wrote about this polyhedron (Spanish translation):
"Otro cuerpo muy distinto de los ya nombrados, Excelso Duque, es el llamado cuerpo de veintiséis bases, de hermosísimo principio y
origen derivado. De sus veintiséis bases, dieciocho son cuadradas, equiláteras y rectángulas, y ocho triangulares, igualmente
equiláteras y equiángulas. Tiene cuarenta y ocho lados o líneas y noventa y seis ángulos superficiales, setenta y dos de los
cuales son rectos -los de sus dieciocho bases cuadradas- y veinticuatro agudos -los de sus ocho triángulos equiláteros-.
Estos noventa y seis ángulos superficiales determinan la formación de dicho cuerpo de veinticuatro ángulos sólidos, cada uno
de los cuales consta de un ángulo superficial del triángulo y tres ángulos rectos de tres cuadrados. Y de sus cuarenta y ocho
líneas, veinticuatro son comunes a los triángulos y a los cuadrados, ya que de sus dieciocho cuadrados, debidamente unidos entre
sí, resultan necesariamente los ocho triángulos, como se ha dicho a proposito de los otros abcisos. El origen de este cuerpo
es el hexaedro uniformemente cortado en todas sus partes, como nos muestra a la vista su propia forma material. Su conocimiento
resulta utilísimo por muchas consideraciones para quien bien lo sepa aplicar, sobre todo en arquitectura. Y esto por lo que
respecta al conocimiento de su sólido plano o hueco."
('La divina proporción' de Luca Pacioli, page 97, Spanish translation by Juan Calatrava, Editorial Akal, 4th edition, 2008)
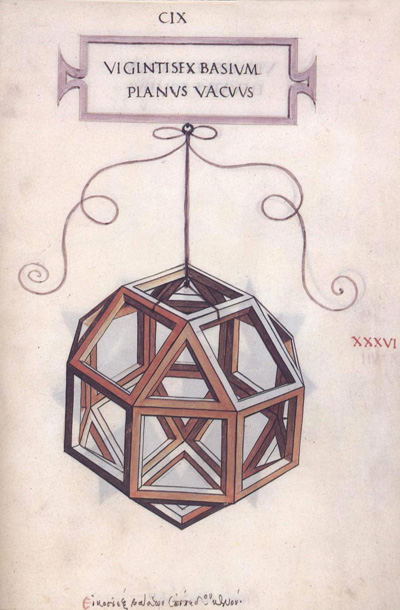
Leonardo da Vinci's drawing of the rhombicuboctahedron
or small rhombicuboctahedron (Vigintisex basium planus vacuus) for Luca Pacioli's book 'De divina proportione'. (There is an Spanish version, 'La divina proporción' Editorial Akal. Image used with permission of Editorial Akal).

Leonardo da Vinci's drawing of the rhombicuboctahedron
or small rhombicuboctahedron (Vigintisex basium planus solidus) for Luca Pacioli's book 'De divina proportione'. (There is an Spanish version, 'La divina proporción' Editorial Akal. Image used with permission of Editorial Akal).
In the interactive application you can rotate the polyhedron and play with the "hole" in each face:




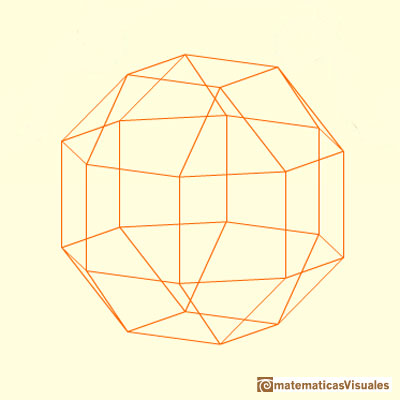
It is easy to build a rhombicuboctahedron with cardboard:

Using cardboard you can build beautiful polyhedra cutting polygons and glue them toghether. This is a very simple and effective technique. You can download several templates. Then print, cut and glue: very easy!



We can build a rhombicuboctahedron with Microarquitectura

Microarquitectura is a construction game developed by Sara San Gregorio. You can play and build a lot of structures modelled on polyhedra.


Edam (Holland), 2016

Barcelona, 2018

Variation about a rhombicuboctahedron in Sauveterre-de-Béarn (Francia), 2018
This beautiful dice is based on the rhombicuboctahedron. It is called the dice of Charles V and you can see it in the Museo Lázaro Galdiano (Madrid, Spain). Ángel Requena wrote a reference of this item in his web site Turismo Matemático. He also wrote an article about this polyhedric dice.

Museo Lázaro Galdiano (Madrid, Spain), 2018
Sundial in the Deutsches Museum in Munich. Its shape is a rhombicuboctahedron.

Sundial in the Deutsches Museum (Munich, Germany), 2016

Sundial in the Deutsches Museum (Munich, Germany), 2016

Sundial in the Deutsches Museum (Munich, Germany), 2016
REFERENCES
Luca Pacioli - La divina proporción - Ediciones Akal, 4th edition, 2004. Spanish edition of 'De divina proportione'. Translation by Juan Calatrava.
Leonardo da Vinci's Geometric Sketches Frank J. Swetz's article in MathDl, Loci:Convergence.
Leonardo da Vinci's Polyhedra George Hart's excellent website about polyhedra.
Ángel Requena's web site Turismo Matemático.
Dan Pedoe - Geometry and the Liberal Arts - St. Martin's Press.
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition.
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS

We can see the interior of the augmented rhombicuboctahedron. Luca Pacioli wrote that you 'can see the interior only with your imagination'.

This polyhedron is also called Elongated Square Gyrobicupola. It is similar to the Rhombicuboctahedron but it is less symmetric.

Starting with a Rhombicubotahedron we can add pyramids over each face. The we get a beautiful polyhedron that it is like a star.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated tetrahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the Campanus' sphere.

You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.

The first drawing of a plane net of a regular octahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Using cardboard you can build beautiful polyhedra cutting polygons and glue them toghether. This is a very simple and effective technique. You can download several templates. Then print, cut and glue: very easy!

Material for a session about polyhedra (Zaragoza, 7th November 2014). We study the octahedron and the tetrahedron and their volumes. The truncated octahedron helps us to this task. We build a cubic box with cardboard and an origami tetrahedron.

Material for a session about polyhedra (Zaragoza, 23rd Octuber 2015) . Building a cube with cardboard and an origami octahedron.

Material for a session about polyhedra (Zaragoza, 9th May 2014). Simple techniques to build polyhedra like the tetrahedron, octahedron, the cuboctahedron and the rhombic dodecahedron. We can build a box that is a rhombic dodecahedron.

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.

The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.