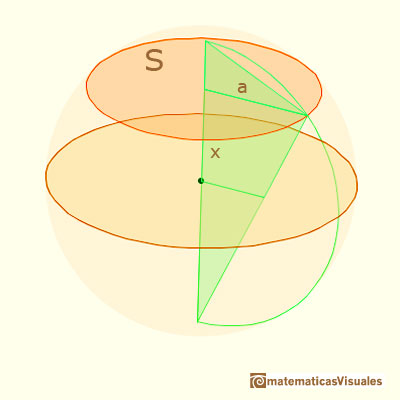
In the initial position of the applet it represents a circle, and when you move the cursor the vertical position of a segment changes.

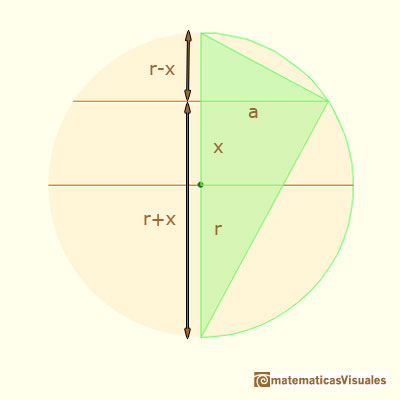
When the vertical position (x) changes we want to calculate the segment a:

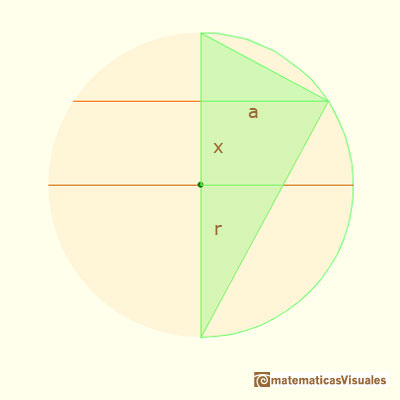
Because our goal is to calculate the surface of the section of the sphere when we change the distance from the center of the sphere to the section. You can see and rotate the sphere clicking and dragging over the applet.

Using the Pythagorean Theorem we can calculate the radius of the section:

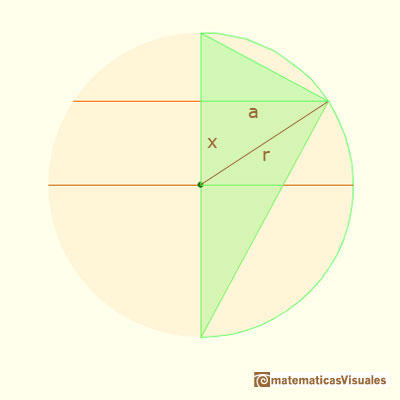
Then the surface of the section of the sphere is:

Then our goal is achieved, but we can have another approach to calculate the chord (or radius, a) without using the Pythagorean Theorem. And this approach will permit us to use similarity of triangles and to talk about the Geometric Mean.

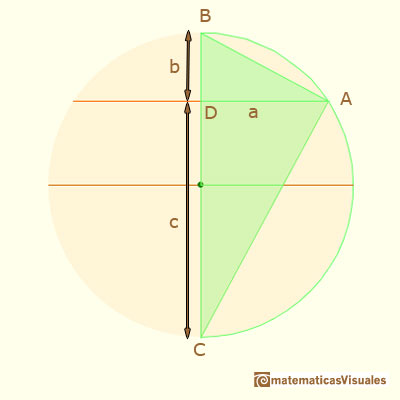
We have three right triangles that are similar. We are interested in two of them:

We can write the proportion (we want to know the value of a):

Then, the value of a is:

We say that a is the Geometric Mean of two numbers, b and c. This result is also called the Right Triangle Altitude Theorem.

The geometric mean of two positive numbers is related with the arithmetic mean:

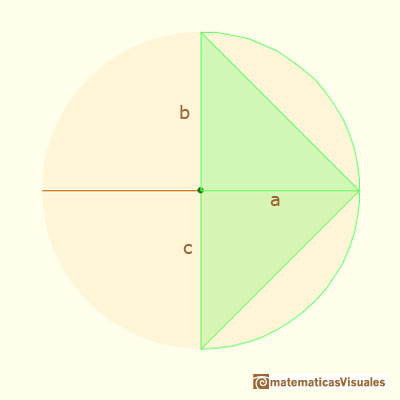
When are the geometric mean equals to the arithmetic mean?

Coming back to our initial subject:

We are going to use this result in two interesting applications of Cavalieri's Theorem: How to calculate the volume of a sphere and Two Surprising Theorems on Cavalieri Congruence one article by Howard Eves in which he constructed a tetrahedron and he used Cavalieri's Theorem to calculate the volume of a sphere.

You can play with these two applets about cross-sections of a sphere:

MORE LINKS

The volume of the tetrahedron

The volume of a tetrahedron is one third of the prism that contains it.

Sections in Howard Eves's tetrahedron

In his article 'Two Surprising Theorems on Cavalieri Congruence' Howard Eves describes an interesting tetrahedron. In this page we calculate its cross-section areas and its volume.

Cavalieri: The volume of a sphere

Using Cavalieri's Principle we can calculate the volume of a sphere.

Kepler: The Area of a Circle

Kepler used an intuitive infinitesimal approach to calculate the area of a circle.

Pythagoras Theorem: Euclid's demonstration

Demonstration of Pythagoras Theorem inspired in Euclid.

Plane developments of geometric bodies: Tetrahedron

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Archimedes and the area of an ellipse: an intuitive approach

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.

Archimedes and the area of an ellipse: Demonstration

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.

Archimedes' Method to calculate the area of a parabolic segment

Archimedes show us in 'The Method' how to use the lever law to discover the area of a parabolic segment.

Campanus' sphere and other polyhedra inscribed in a sphere

We study a kind of polyhedra inscribed in a sphere, in particular the Campanus' sphere that was very popular during the Renaissance.

Leonardo da Vinci:Drawing of a SEPTUAGINTA made to Luca Pacioli's De divina proportione.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the Campanus' sphere.