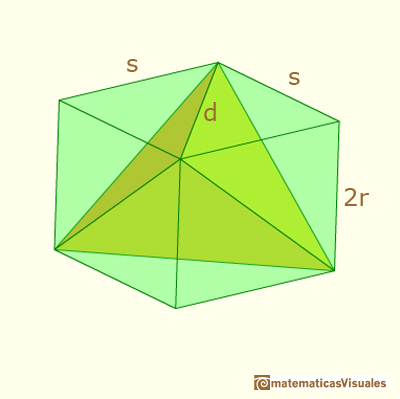
Howard Eves describes a tetrahedron as follows:

... draw two line segments AB and CD perpendicular to one another, each of length

and having the line segment joining their midpoints as a common perpendicular. "

The distance between these two lines is 2r.

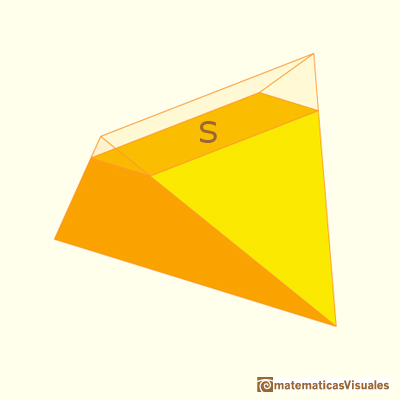
This tetrahedron can be considered within a prism of a square base and height 2r.

The side of the square is

Therefore, the volume of the tetrahedron is

If x is the distance from the plane of the section that represents the applet to the center of the tetrahedron, the area of the section is (this is a particular case of sections of a tetrahedron):

Now that we now how to calculate the volume of a tetrahedron and the cross-sections areas of a tetrahedron and a sphere we can see how Howard Eves mixed all these ideas to calculate the volume of a sphere using Cavalieri's Principle.

MORE LINKS

The volume of the tetrahedron

The volume of a tetrahedron is one third of the prism that contains it.

Sections in the sphere

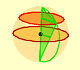
We want to calculate the surface area of sections of a sphere using the Pythagorean Theorem. We also study the relation with the Geometric Mean and the Right Triangle Altitude Theorem.

Cavalieri: The volume of a sphere

Using Cavalieri's Principle we can calculate the volume of a sphere.

Campanus' sphere and other polyhedra inscribed in a sphere

We study a kind of polyhedra inscribed in a sphere, in particular the Campanus' sphere that was very popular during the Renaissance.

Sections in the sphere

We want to calculate the surface area of sections of a sphere using the Pythagorean Theorem. We also study the relation with the Geometric Mean and the Right Triangle Altitude Theorem.

Pythagoras Theorem: Euclid's demonstration

Demonstration of Pythagoras Theorem inspired in Euclid.

Leonardo da Vinci:Drawing of a SEPTUAGINTA made to Luca Pacioli's De divina proportione.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the Campanus' sphere.

Cavalieri: The volume of a sphere

Using Cavalieri's Principle we can calculate the volume of a sphere.

Kepler: The Area of a Circle

Kepler used an intuitive infinitesimal approach to calculate the area of a circle.

Plane developments of geometric bodies: Tetrahedron

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Archimedes and the area of an ellipse: an intuitive approach

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.

Archimedes and the area of an ellipse: Demonstration

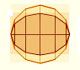
In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.

Archimedes' Method to calculate the area of a parabolic segment

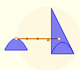
Archimedes show us in 'The Method' how to use the lever law to discover the area of a parabolic segment.