In this page we follow our study of the geometric interpretation of complex numbers as points (or vectors) in the plane.

"The publication of the geometric interpretation by Wessel and by Argand went all but unnoticed, but the reputation of Gauss (as great then as it is now) ensured wide disemination and acceptance of complex numbers as points in the plane. Perhaps less important than the details of this new interpretation (at least initially) was the mere fact that there now existed some way of making sense of these numbers -that they were now legitimate objects of investigation. In any event, the floodgates of invention were about to open." (Needham, 3)

In particular, the product of complex numbers is related with the dilative rotation.

Multiplying two complex numbers

We can see it as a dilatative rotation.

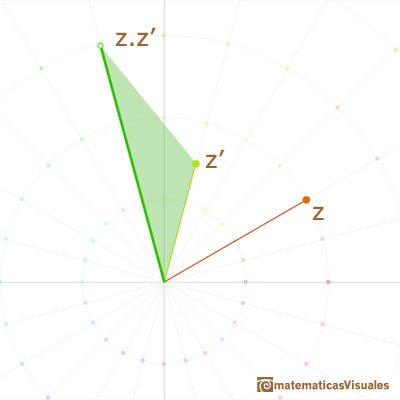
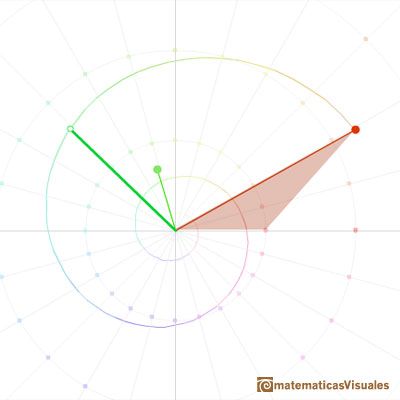
Geometrically, multiplication by a complex number z is a rotation of the plane (the angle is the argument of z) and an expansion of the plane by a factor (this factor is the module or length of z).

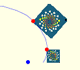
Using Frank Farris' visualization of the complex plane with colors we can see the initial representation:

And the representation of the complex plane after the multiplication by a complex number z.

Rotations and expansions preserve parallelograms. In particular, we can see the transformation of a square into another square.

MORE LINKS

Dilative rotation

A Dilative Rotation is a combination of a rotation an a dilatation from the same point.

Equiangular spiral

In an equiangular spiral the angle between the position vector and the tangent is constant.

Dilation and rotation in an equiangular spiral

Two transformations of an equiangular spiral with the same general efect.