matematicasVisuales|Complex Analysis

Complex Analysis


			$Multifunctions: Powers with fractional exponent \| matematicasVisuales$

Product of complex numbers
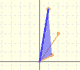	Multiplying two complex numbers We can see it as a dilatative rotation.
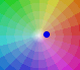	The product as a complex plane transformation The multiplication by a complex number is a transformation of the complex plane: dilative rotation.
	Complex Geometric Sequence From a complex number we can obtain a geometric progression obtaining the powers of natural exponent (multiplying successively)
Complex Functions
	Complex Polynomial Functions(1): Powers with natural exponent Complex power functions with natural exponent have a zero (or root) of multiplicity n in the origin.
	Complex Polynomial Functions(2): Polynomial of degree 2 A polynomial of degree 2 has two zeros or roots. In this representation you can see Cassini ovals and a lemniscate.
	Complex Polynomial Functions(3): Polynomial of degree 3 A complex polinomial of degree 3 has three roots or zeros.
	Complex Polynomial Functions(4): Polynomial of degree n Every complex polynomial of degree n has n zeros or roots.
	Complex Polynomial Functions(5): Polynomial of degree n (variant) Every complex polynomial of degree n has n zeros or roots.
	Cero and polo (Spanish) Podemos modificar las multiplicidades del cero y del polo de estas funciones sencillas.
	Cero and polo (variant) (Spanish)
	Moebius transformations (Spanish) Una primera aproximación a estas transformaciones. Representación de dos haces coaxiales de circunferencias ortogonales.
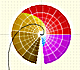	The Complex Exponential Function The Complex Exponential Function extends the Real Exponential Function to the complex plane.
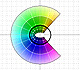	The Complex Cosine Function The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.
	The Complex Cosine Function: mapping an horizontal line The Complex Cosine Function maps horizontal lines to confocal ellipses.
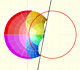	Inversion Inversion is a plane transformation that transform straight lines and circles in straight lines and circles.
	Inversion: an anticonformal transformation Inversion preserves the magnitud of angles but the sense is reversed. Orthogonal circles are mapped into orthogonal circles
$Multifunctions: Powers with fractional exponent \| matematicasVisuales$	Multifunctions: Powers with fractional exponent The usual definition of a function is restrictive. We may broaden the definition of a function to allow f(z) to have many differente values for a single value of z. In this case f is called a many-valued function or a multifunction.
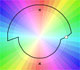	Multifunctions: Two branch points Multifunctions can have more than one branch point. In this page we can see a two-valued multifunction with two branch points.
Taylor's Polynomials
	Taylor polynomials: Rational function with two complex singularities We will see how Taylor polynomials approximate the function inside its circle of convergence.
	Taylor polynomials: Complex Exponential Function The complex exponential function is periodic. His power series converges everywhere in the complex plane.
	Taylor polynomials: Complex Cosine Function The power series of the Cosine Function converges everywhere in the complex plane.