28th February 2022
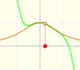
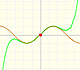
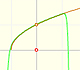
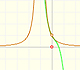
Tetraxis
 |
Tetraxis is a wonderful puzzle designed by Jane and John Kostick. We study some properties of this puzzle and its relations with the rhombic dodecahedron. We can build this puzzle using cardboard and magnets or using a 3D printer.
|
7th January 2019
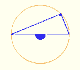
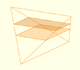
History: Kepler and the volume of a wine barrel (another look)
 |
Kepler was one mathematician who contributed to the origin of integral calculus. He used infinitesimal techniques for calculating areas and volumes. In this page we study one optimization problem.
|
12th November 2018
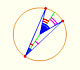
Geometry: Pascal's Theorem
 |
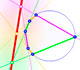If a hexagon is inscribed in a circle, the three pairs of opposite sides meet in collinear points.
|
14th May 2018
History: Durer and the ellipse
 |
Durer was the first who published in german a method to draw ellipses as cone sections.
|
 |
Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .
|
7th May 2018
Geometry: Ellipses
 |
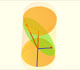The section of a cylinder by a plane cutting its axis at a single point is an ellipse. A beautiful demonstration uses Dandelin Spheres.
|
2nd April 2018
Geometry and History
 |
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the augmented rhombicuboctahedron.
|
 |
We can see the interior of the augmented rhombicuboctahedron. Luca Pacioli wrote that you 'can see the interior only with your imagination'.
|
 |
Starting with a Rhombicubotahedron we can add pyramids over each face. The we get a beautiful polyhedron that it is like a star.
|
12th February 2018
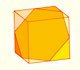
Geometry: Pseudo Rhombicuboctahedron
 |
This polyhedron is also called Elongated Square Gyrobicupola. It is similar to the Rhombicuboctahedron but it is less symmetric.
|
29th January 2018
Geometry: Triangles
 |
Dynamic demonstration of the Pythagorean Theorem by Hermann Baravalle.
|
8th January 2018
Geometry: Triangles
 |
Demonstration of Pythagoras Theorem inspired in Euclid.
|
11th December 2017
Geometry: The World
 |
This perpective projection is area-preserving. If we know the surface area of a sphere we can deduce the volume of a sphere, as Archimedes did.
|
27th November 2017
Geometry: The World
 |
Basic world map in a sphere. Latitude and longitude
|
19th November 2017
Geometry: Campanus' sphere
 |
We study a kind of polyhedra inscribed in a sphere, in particular the Campanus' sphere that was very popular during the Renaissance.
|
13th November 2017
History: Leonardo da Vinci
 |
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the Campanus' sphere.
|
25th September 2017
Geometry: Building polyhedra
 |
Material for a session about polyhedra (Zaragoza, el 20th October 2017). Instruction to build an origami tetrahedron.
|
18th September 2017
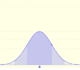
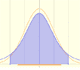
Probability: Normal Distributions
 |
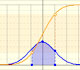Calculating probabilities of symmetric intervals around the mean of a normal distribution.
|
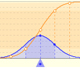
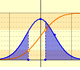
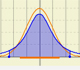
11th September 2017
Probability: Normal Distributions
 |
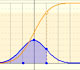The (cumulative) distribution function of a random variable X, evaluated at x, is the probability that X will take a value less than or equal to x. In this page we study the Normal Distribution.
|
5th June 2017
Geometry: Rhombic Dodecahedron
 |
A chain of six pyramids can be turned inwards to form a cube or turned outwards, placed over another cube to form the rhombic dodecahedron.
|
15th May 2017
Geometry: Building polyhedra
 |
Microarquitectura is a construction game developed by Sara San Gregorio. You can play and build a lot of structures modelled on polyhedra.
|
3rd May 2017
Geometry: Rhombic Dodecahedron
 |
The Rhombic Dodecahedron fills the space without gaps.
|
3rd April 2017
Geometry: Rhombic Dodecahedron
 |
You can build a Rhombic Dodecahedron adding six pyramids to a cube. This fact has several interesting consequences.
|
6th March 2017
Geometry: Rhombic Dodecahedron
 |
Adding six pyramids to a cube you can build new polyhedra with twenty four triangular faces. For specific pyramids you get a Rhombic Dodecahedron that has twelve rhombic faces.
|
20th February 2017
Geometry: Building polyhedra
 |
Building cubes and octahedra using 3d printing. Cube and Octahedron are dual polyhedra.
|
6th February 2017
Geometry: Rhombic Dodecahedron
 |
We want to close a hexagonal prism as bees do, using three rhombi. Then, which is the shape of these three rhombi that closes the prism with the minimum surface area?.
|
16th January 2017
Geometry: Building polyhedra
 |
Building tetraedra using 3d printing. The tetrahedron is a self-dual polyhedron. The center of a tetrahedron.
|
9th January 2017
Geometry: Rhombic Dodecahedron
 |
Humankind has always been fascinated by how bees build their honeycombs. Kepler related honeycombs with a polyhedron called Rhombic Dodecahedron.
|
5th December 2016
Geometry and Art: Bruno Munari
 |
Italian designer Bruno Munari conceived 'Acona Biconbi' as a work of sculpture. It is also a beautiful game to play with colors and shapes.
|
21st November 2016
Geometry: Building polyhedra
 |
Simple technique to build polyhedra gluing discs made of cardboard or paper.
|
7th November 2016
Geometry: Curves
 |
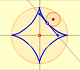The Astroid is a particular case of a family of curves called hypocycloids.
|
19th September 2016
Geometry: Polyhedra
 |
Material for a session about polyhedra (Zaragoza, 21st October 2016). Instructions to build several geometric bodies.
|
5th September 2016
Geometry: Curves
 |
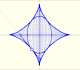The Astroid is the envelope of a segment of constant length moving with its ends upon two perpendicular lines. It is also the envelope of a family of ellipses, the sum of whose axes is constant.
|
1st August 2016
Geometry: Ellipses
 |
If a straight-line segment is moved in such a way that its extremities travel on two mutually perpendicular straight lines then the midpoint traces out a circle; every other point of the line traces out an ellipse.
|
4th July 2016
Geometry: Ellipses
 |
An Ellipsograph is a mechanical device used for drawing ellipses.
|
6th June 2016
Geometry: Pyritohedron
 |
If you fold the six roofs of a regular dodecahedron into a cube there is an empty space. This space can be filled with an irregular dodecahedron composed of identical irregular pentagons (a kind of pyritohedron).
|
2nd May 2016
Geometry: Dodecahedron and cube
 |
A Cube can be inscribed in a Dodecahedron. A Dodecahedron can be seen as a cube with six 'roofs'. You can fold a dodecahedron into a cube.
|
4th April 2016
History: Leonardo da Vinci
 |
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the rhombicuboctahedron.
|
7th March 2016
Geometry: Plane net of a tetrahedron
 |
The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
|
1st February 2016
Geometry: Plane net of an octahedron
 |
The first drawing of a plane net of a regular octahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
|
18th January 2016
History: Leonardo da Vinci
 |
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the octahedron.
|
31st December 2015
Complex Update: Multiplication of Complex Numbers
 |
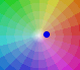The multiplication by a complex number is a transformation of the complex plane: dilative rotation.
|
7th December 2015
Complex Update: Multiplication of Complex Numbers
 |
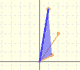We can see it as a dilatative rotation.
|
16th November 2015
Analysis Update: Geometric sequences
 |
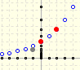Geometric sequences graphic representations. Sum of terms of a geometric sequence and geometric series.
|
2nd November 2015
History: Durer and transformations of faces
 |
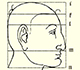He studied transformations of images, for example, faces.
|
28th September 2015
Geometry: Polyhedra
 |
Material for a session about polyhedra (Zaragoza, 23rd Octuber 2015) . Building a cube with cardboard and an origami octahedron.
|
21th September 2015
Geometry: Triangles
 |
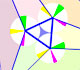Interactive animation about John Conway's beautiful proof of Morley's Theorem
|
14th September 2015
Geometry Updates: Triangles
 |
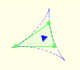Steiner Deltoid and the Morley triangle are related.
|
7th September 2015
Geometry Updates: Triangles
 |
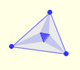The three points of intersection of the adjacent trisectors of the angles of any triangle are the vertices of an equilateral triangle (Morley's triangle)
|
29th June 2015
Geometry Updates: Triangles
 |
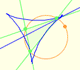The Simson-Wallace lines of a triangle envelops a curve called the Steiner Deltoid.
|
8th June 2015
Geometry Updates: Triangles
 |
Interactive demonstration of the Wallace-Simson line.
|
6th April 2015
Geometry: Spirals
 |
There are infinitely many equiangular spirals through two given points.
|
2nd March 2015
Analysis: Piecewise Functions
 |
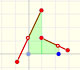Graphs of these functions are made of disconnected line segments. There are points where a small change in x produces a sudden jump in the value of the function.
|
2nd February 2015
Analysis: Piecewise Functions
 |
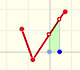A continuous piecewise linear function is defined by several segments or rays connected, without jumps between them.
|
12th January 2015
Analysis: Piecewise Functions
 |
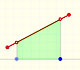As an introduction to Piecewise Linear Functions we study linear functions restricted to an open interval: their graphs are like segments.
|
1st December 2014
Analysis: Piecewise Functions
 |
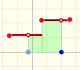A piecewise function is a function that is defined by several subfunctions. If each piece is a constant function then the piecewise function is called Piecewise constant function or Step function.
|
27th October 2014
Geometry: Polyhedra
 |
Material for a session about polyhedra (Zaragoza, 7th November 2014). We study the octahedron and the tetrahedron and their volumes. The truncated octahedron helps us to this task. We build a cubic box with cardboard and an origami tetrahedron.
|
20th October 2014
Geometry: Polyhedra
 |
Using cardboard you can build beautiful polyhedra cutting polygons and glue them toghether. This is a very simple and effective technique. You can download several templates. Then print, cut and glue: very easy!
|
6th October 2014
Geometry: Polyhedra
 |
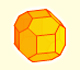You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.
|
7th July 2014
Geometry: Polyhedra
 |
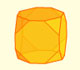When you truncate a cube you get a truncated cube and a cuboctahedron. If you truncate an octahedron you get a truncated octahedron and a cuboctahedron.
|
2nd June 2014
Geometry: Polyhedra
 |
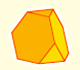The truncated tetrahedron is an Archimedean solid made by 4 triangles and 4 hexagons.
|
27th April 2014
Geometry: Building Polyhedra, cuboctahedron and rhombic dodecahedron (Spanish)
 |
Material for a session about polyhedra (Zaragoza, 9th May 2014). Simple techniques to build polyhedra like the tetrahedron, octahedron, the cuboctahedron and the rhombic dodecahedron. We can build a box that is a rhombic dodecahedron.
|
7th April 2014
History: Leonardo da Vinci
 |
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated tetrahedron.
|
3rd March 2014
Analysis: Rational Functions
 |
You can add a polynomial to a proper rational function. The end behavior of this rational function is very similar to the polynomial.
|
3rd February 2014
Analysis: Rational Functions
 |
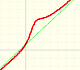For large absolute values of x, some rational functions behave like an oblique straight line, we call this line an oblique or slant asymptote.
|
7th January 2014
Analysis: Rational Functions
 |
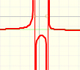When the denominator of a rational function has degree 2 the function can have two, one or none real singularities.
|
2nd December 2013
Analysis: Rational Functions
 |
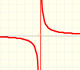Rational functions can be writen as the quotient of two polynomials. Linear rational functions are the simplest of this kind of functions.
|
20th October 2013
Analysis: Convergence of Series, the Integral Test
 |
Using a decreasing positive function you can define series. The integral test is a tool to decide if a series converges o diverges. If a series converges, the integral test provide us lower and upper bounds.
|
7th October 2013
History: Durer's construction of a non regular pentagon
 |
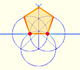In his book 'Underweysung der Messung' Durer draw a non-regular pentagon with ruler and a fixed compass. It is a simple construction and a very good approximation of a regular pentagon.
|
16th September 2013
Geometry: Plane net of a dodecahedron
 |
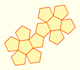The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
|
2nd September 2013
Geometry: Volume of a regular dodecahedron
 |
One eighth of a regular dodecahedon of edge 2 has the same volume as a dodecahedron of edge 1.
|
1st July 2013
Geometry: Drawing a regular pentagon
 |
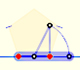You can draw a regular pentagon given one of its sides constructing the golden ratio with ruler and compass.
|
3rd June 2013
Geometry: Fifteen degrees angle
 |
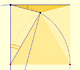Using a ruler and a compass we can draw fifteen degrees angles. These are basic examples of the central and inscribed in a circle angles property.
|
6th May 2013
Geometry: The Golden Ratio
 |
The diagonal of a regular pentagon are in golden ratio to its sides and the point of intersection of two diagonals of a regular pentagon are said to divide each other in the golden ratio or 'in extreme and mean ratio'.
|
1st April 2013
Analysis: The Fundamental Theorem of Calculus
 |
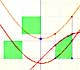The Second Fundamental Theorem of Calculus is a powerful tool for evaluating definite integral (if we know an antiderivative of the function).
|
4th March 2013
Analysis: The Fundamental Theorem of Calculus
 |
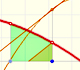The Fundamental Theorem of Calculus tell us that every continuous function has an antiderivative and shows how to construct one using the integral.
|
18th February 2013
Analysis: Powers and Polynomials
 |
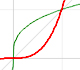Power with natural exponents are simple and important functions. Their inverse functions are power with rational exponents (a radical or a nth root)
|
3th February 2013
Analysis: Integral
 |
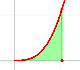The integral of power functions was know by Cavalieri from n=1 to n=9. Fermat was able to solve this problem using geometric progressions.
|
3th January 2013
Analysis: Integral
 |
Monotonic functions in a closed interval are integrable. In these cases we can bound the error we make when approximating the integral using rectangles.
|
3th December 2012
Analysis: Integral
 |
If we consider the lower limit of integration a as fixed and if we can calculate the integral for different values of the upper limit of integration b then we can define a new function: an indefinite integral of f.
|
12th November 2012
Analysis: Integral
 |
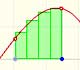The integral concept is associated to the concept of area. We began considering the area limited by the graph of a function and the x-axis between two vertical lines.
|
22th October 2012
Analysis: Polynomial functions and derivative
 |
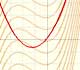If the derivative of F(x) is f(x), then we say that an indefinite integral of f(x) with respect to x is F(x). We also say that F is an antiderivative or a primitive function of f.
|
1st October 2012
Analysis: Powers and polynomials
 |
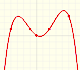We can consider the polynomial function that passes through a series of points of the plane. This is an interpolation problem that is solved here using the Lagrange interpolating polynomial.
|
17th September 2012
Analysis: Polynomial functions and integral
 |
We can see some basic concepts about integration applied to a general polynomial function. Integral functions of polynomial functions are polynomial functions with one degree more than the original function.
|
27th August 2012
Analysis: Polynomial functions and integral
 |
To calculate the area under a parabola is more difficult than to calculate the area under a linear function. We show how to approximate this area using rectangles and that the integral function of a polynomial of degree 2 is a polynomial of degree 3.
|
6th August 2012
Analysis: Polynomial functions and integral
 |
It is easy to calculate the area under a straight line. This is the first example of integration that allows us to understand the idea and to introduce several basic concepts: integral as area, limits of integration, positive and negative areas.
|
18th June 2012
Analysis: Polynomial functions and derivative
 |
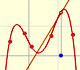Lagrange polynomials are polynomials that pases through n given points. We use Lagrange polynomials to explore a general polynomial function and its derivative.
|
28th May 2012
Analysis: Polynomial functions and derivative
 |
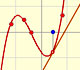The derivative of a cubic function is a quadratic function, a parabola.
|
7th May 2012
Analysis: Polynomial functions and derivative
 |
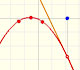The derivative of a quadratic function is a linear function, it is to say, a straight line.
|
16th April 2012
Analysis: Polynomial functions and derivative
 |
The derivative of a lineal function is a constant function.
|
20th March 2012
Geometry: Building polyhedra. Simple techniques
 |
Several pages about simple techniques for building polyhedra: cardboard, origami, tubes, zome, tensegrity.
|
20th February 2012
Geometry: Plane developments of geometric bodies
 |
Plane developments of cones cut by an oblique plane. The section is an ellipse.
|
30th January 2012
Geometry: Plane developments of geometric bodies
 |
Plane developments of cones and conical frustum. How to calculate the lateral surface area.
|
9th January 2012
Geometry: Plane developments of geometric bodies
 |
Plane net of pyramids cut by an oblique plane.
|
2nd December 2011
Geometry: Plane developments of geometric bodies
 |
Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.
|
18th November 2011
Personal: The Game of Life with Nature photos
 |
In this new version of The Game of Life invented by John H. Conway we can see more than 100 new photos of Nature. Each time you run the application, 36 photos randomly choosen are shown.
|
4th November 2011
Geometry: Plane developments of geometric bodies
 |
We study different cylinders cut by an oblique plane. The section that we get is an ellipse.
|
21st October 2011
Geometry: Plane developments of geometric bodies
 |
We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.
|
7th October 2011
Geometry: Plane developments of geometric bodies
 |
Plane nets of prisms with a regular base with different side number cut by an oblique plane.
|
30th September 2011
Geometry: Plane developments of geometric bodies
 |
We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.
|
15th September 2011
Analysis
 |
New version of several pages about Taylor Polynomial with improved mathlets and more images. We start studying several real functions but we need to go to the complex plane to get a better understandig of the concept.
|
30th August 2011
Probability
 |
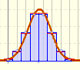In some cases, a Binomial distribution can be approximated by a Normal distribution with the same mean and variance.
|
3rd August 2011
Probability
 |
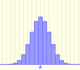When modeling a situation where there are n independent trials with a constant probability p of success in each test we use a binomial distribution.
|
26th June 2011
Geometry
 |
We want to calculate the surface area of sections of a sphere using the Pythagorean Theorem. We also study the relation with the Geometric Mean and the Right Triangle Altitude Theorem. We use this result in some applications of Cavalieri's Theorem.
|
29th May 2011
History: Archimedes and the area of the ellipse
 |
In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.
|
 |
In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.
|
29th May 2011
Geometry: Ellipses
 |
Transforming a circle we can get an ellipse (as Archimedes did to calculate its area). From the equation of a circle we can deduce the equation of an ellipse.
|
 |
Every ellipse has two foci and if we add the distance between a point on the ellipse and these two foci we get a constant.
|
29th April 2011
Drawings of Leonardo da Vinci for Luca Pacioli's book 'De divine proportione'
 |
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.
|
 |
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.
|
 |
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.
|
 |
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).
|
29th April 2011
Volume of polyhedra
 |
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.
|
 |
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.
|
 |
The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.
|
 |
The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.
|
24th February 2011
Geometry
 |
There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.
|
21st January 2011
Geometry
 |
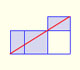From Euclid's definition of the division of a segment into its extreme and mean ratio we introduce a property of golden rectangles and we deduce the equation and the value of the golden ratio.
|
5th January 2011
Circles
 |
Central angle in a circle is twice the angle inscribed in the circle.
|
 |
Interactive 'Mostation' of the property of central and inscribed angles in a circle. Case I: When the arc is half a circle the inscribed angle is a right angle.
|
 |
Interactive 'Mostation' of the property of central and inscribed angles in a circle. Case II: When one chord that forms the inscribed angle is a diameter.
|
 |
Interactive 'Mostation' of the property of central and inscribed angles in a circle. The general case is proved.
|
18th September 2010
Complex Functions
 |
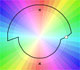Multifunctions can have more than one branch point. In this page we can see a two-valued multifunction with two branch points.
|
26th July 2010
Geometry
 |
The volume of a tetrahedron is one third of the prism that contains it.
|
15th July 2010
Complex Functions
 |
The usual definition of a function is restrictive. We may broaden the definition of a function to allow f(z) to have many differente values for a single value of z. In this case f is called a many-valued function or a multifunction.
|
11th June 2010
Geometry
 |
The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron
|
7th June 2010
Geometry
 |
We can cut in half a cube by a plane and get a section that is a regular hexagon. Using eight of this pieces we can made a truncated octahedron.
|
 |
Using eight half cubes we can make a truncated octahedron. The cube tesselate the space an so do the truncated octahedron. We can calculate the volume of a truncated octahedron.
|
2nd June 2010
Analysis
 |
The geometric series of ratio 1/2 is convergent. We can represent this series using a rectangle and cut it in half successively. Here we use a rectangle such us all rectangles are similar.
|
25th May 2010
Analysis
 |
One intuitive example of how to sum a geometric series. In this case, we study the geometric series with ratio equal 1/4.
|
7th May 2010
Geometry
 |
These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.
|
28th April 2010
Geometry
 |
The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
|
23th April 2010
Geometry
 |
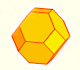The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
|
17th March 2010
Complex Functions
 |
The Complex Cosine Function maps horizontal lines to confocal ellipses.
|
28th February 2010
History
 |
Kepler used an intuitive infinitesimal approach to calculate the area of a circle.
|
19th February 2010
Complex Functions
 |
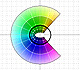The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.
|
5th February 2010
History
 |
Using Cavalieri's Principle we can calculate the volume of a sphere.
|
8th January 2010
History
 |
Kepler was one mathematician who contributed to the origin of integral calculus. He used infinitesimal techniques for calculating areas and volumes.
|
8th December 2010
History
 |
Studying the volume of a barrel, Kepler solved a problem about maxima in 1615.
|
21th November 2009
History
 |
Mercator published his famous series for the Logarithm Function in 1668. Euler discovered a practical series to calculate.
|
16th November 2009
History
 |
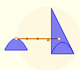Archimedes show us in 'The Method' how to use the lever law to discover the area of a parabolic segment.
|
26th Octuber 2009
History
 |
We can see Pythagoras' Theorem in a tiling. It is a graphic demonstration of Pythagoras' Theorem we can see in some floor made using squares of two different sizes.
|
14th October 2009
Complex Functions
 |
Inversion preserves the magnitud of angles but the sense is reversed. Orthogonal circles are mapped into orthogonal circles
|
6th October 2009
Complex Functions
 |
Inversion is a plane transformation that transform straight lines and circles in straight lines and circles.
|
22th September 2009
Complex Functions
 |
The Complex Exponential Function extends the Real Exponential Function to the complex plane.
|
14th September 2009
Personal
|
|
In this new version of The Game of Life invented by John H. Conway we can see more than 100 photos of Nature.
|
1st September 2009
Taylor Polynomials
 |
The complex exponential function is periodic. His power series converges everywhere in the complex plane.
|
 |
The power series of the Cosine Function converges everywhere in the complex plane.
|
15th June 2009
Taylor Polynomials
 |
This function has two real singularities at -1 and 1. Taylor polynomials approximate the function in an interval centered at the center of the series. Its radius is the distance to the nearest singularity.
|
 |
This is a continuos function and has no real singularities. However, the Taylor series approximates the function only in an interval. To understand this behavior we should consider a complex function.
|
 |
We will see how Taylor polynomials approximate the function inside its circle of convergence.
|
23th May 2009
Taylor Polynomials
|
|
By increasing the degree, Taylor polynomial approximates the exponential function more and more.
|
 |
By increasing the degree, Taylor polynomial approximates the sine function more and more.
|
 |
The function is not defined for values less than -1. Taylor polynomials about the origin approximates the function between -1 and 1.
|
 |
The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.
|
 |
The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.
|
8th May 2009
Personal, new section
|
|
Te Game of Life was invented by John H. Conway. It is one of the most famous bidimensional cellular automaton. Using a colony we can see some photographs about Nature.
|
28th February 2009
Space Geometry
 |
Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.
|
26th January 2009
Transformations
|
|
He studied transformations of images, for example, faces.
|
 |
In this painting we can see, among lots of interesting things, an anamorphosis of a skull. (In Spanish)
|
19th January 2009
Space Geometry
|
|
The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
|
10th January 2009
Sequences and Series
 |
Gamma, the Euler's constant, is defined using a covergent series.
|
17th November 2008
Space Geometry
|
|
Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.
|
|
|
One eighth of a regular dodecahedon of edge 2 has the same volume as a dodecahedron of edge 1.
|
8th November 2008
Space Geometry
|
|
The volume of a tetrahedron is one third of the prism that contains it.
|
 |
Special sections of a tetrahedron are rectangles (and even squares). We can calculate the area of these cross-sections.
|
 |
In his article 'Two Surprising Theorems on Cavalieri Congruence' Howard Eves describes an interesting tetrahedron. In this page we calculate its cross-section areas and its volume.
|
|
|
We want to calculate the surface area of sections of a sphere using the Pythagorean Theorem. We also study the relation with the Geometric Mean and the Right Triangle Altitude Theorem.
|
 |
Howard Eves's tetrahedron is Cavalieri congruent with a given sphere. You can see that corresponding sections have the same area. Then the volumen of the sphere is the same as the volume of the tetrahedron. And we know how to calculate this volumen.
|
12th August 2008
Random Variables
|
|
When modeling a situation where there are n independent trials with a constant probability p of success in each test we use a binomial distribution.
|
 |
Poisson distribution is discrete (like the binomial) because the values that can take the random variable are natural numbers, although in the Poisson distribution all the possible cases are theoretically infinite.
|
 |
The Normal distribution was studied by Gauss. This is a continuous random variable (the variable can take any real value). The density function is shaped like a bell.
|
 |
One important property of normal distributions is that if we consider intervals centered on the mean and a certain extent proportional to the standard deviation, the probability of these intervals is constant regardless of the mean and standard deviation of the normal distribution considered.
|
 |
It may be interesting to familiarize ourselves with the probabilities correspondig to different intervals in normal distributions.
|
 |
Student's t-distributions were studied by William Gosset(1876-1937) when working with small samples.
|
 |
|
4th August 2007
MatematicasVisuales first English version.