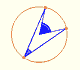
Matematicas Visuales | Central and inscribed angles in a circle | Mostration

Central and inscribed angles in a circle

Central angle in a circle is twice the angle inscribed in the circle.

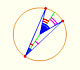
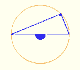
CASE 2. When the vertex is one of the ends of the diameter and the cord draws up from the other end, the angle in center is the double of the angle in the vertex.

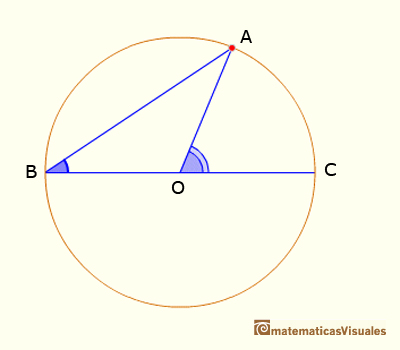
Central Angle Theorem Case II | matematicasvisuales

In this case we want to prove that

We draw the line OP parallel to AB, and then

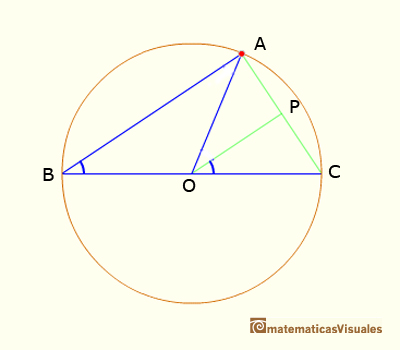
Central Angle Theorem Case II Step 1 | matematicasvisuales

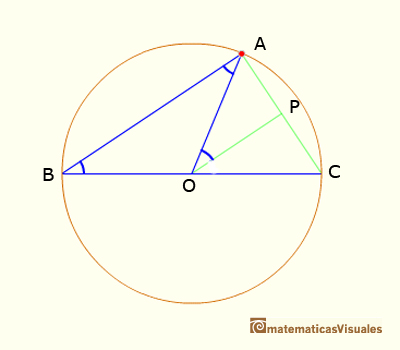
Central Angle Theorem Case II Step 2 | matematicasvisuales

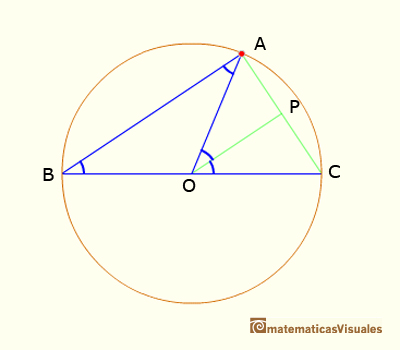
Central Angle Theorem Case II Step 3 | matematicasvisuales

Adding this two angles we get the result:

Now is very easy to probe the general case. You can see an interactive demostration of the Central and inscribed angles in a circle | General Case.

REFERENCES

Euclides, The Elements

next NEXT

Central and inscribed angles in a circle | Mostration | General Case

Interactive 'Mostation' of the property of central and inscribed angles in a circle. The general case is proved.

Central and inscribed angles in a circle | Mostration | Case I

Interactive 'Mostation' of the property of central and inscribed angles in a circle. Case I: When the arc is half a circle the inscribed angle is a right angle.

MORE LINKS

Central and inscribed angles in a circle

Central angle in a circle is twice the angle inscribed in the circle.

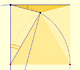
Drawing fifteen degrees angles

Using a ruler and a compass we can draw fifteen degrees angles. These are basic examples of the central and inscribed in a circle angles property.

Pythagoras Theorem: Euclid's demonstration

Demonstration of Pythagoras Theorem inspired in Euclid.

Wallace-Simson lines

Each point in the circle circunscribed to a triangle give us a line (Wallace-Simson line)

Wallace-Simson lines | Demonstration

Interactive demonstration of the Wallace-Simson line.

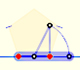
Drawing a regular pentagon with ruler and compass

You can draw a regular pentagon given one of its sides constructing the golden ratio with ruler and compass.

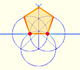
Durer's approximation of a Regular Pentagon

In his book 'Underweysung der Messung' Durer draw a non-regular pentagon with ruler and a fixed compass. It is a simple construction and a very good approximation of a regular pentagon.

The Diagonal of a Regular Pentagon and the Golden Ratio

The diagonal of a regular pentagon are in golden ratio to its sides and the point of intersection of two diagonals of a regular pentagon are said to divide each other in the golden ratio or 'in extreme and mean ratio'.