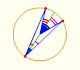
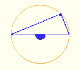
Given two points on a circle, lines from them to the center of the circle form the central angle.
The inscribed angle is the angle subtended at a point on the circle by two given points on the circle. An inscribed angle is defined by two chords of the circle sharing an end point.
Euclid enumerates several propositions about a circle, for example:
III.20. In a circle the angle at the center is double the angle at the circunference, when the rays forming the angles meet the circunference in the same two points.
This is the Central Angle Theorem: The central angle subtended by two points on a circle is twice the inscribed angle subtended by those points.
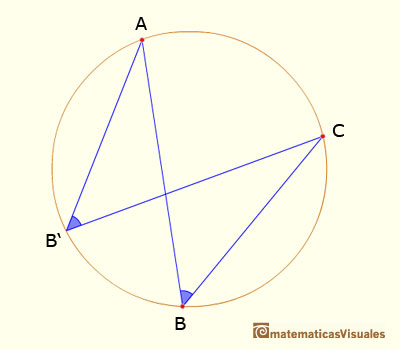
III.21. In a circle, a chord subtends equal angles at any two points on the same one of the two arcs determined by the chord.
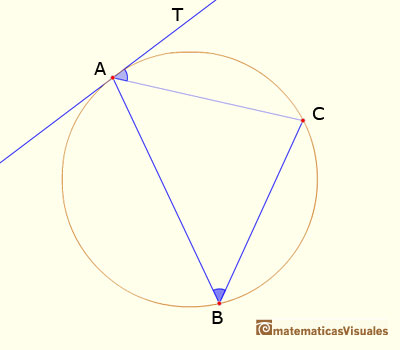
III.32. If a chord of a circle be drawn from the point of contact of a tangent, the angle made by the chord with the tangent is equal to the angle subtended by the chord at a point on that part of the circunference which lies on the far side of the chord.
The demostration of the Central Angle Theorem can be done distinguishing several cases. To start with you can see an interactive approach to a demostration of the Central and inscribed angles in a circle |Case I.
REFERENCES
 NEXT
NEXT
MORE LINKS