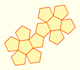
The first time I read about this amazing construction of a non-regular pentagon by Dürer was in Dan Pedoe's book 'Geometry and the Liberal Arts' (an Spanish version was published by Gustavo Gili Editores in 1979).
As Pedoe pointed out 'Dürer's interest in the construction of regular polygons is a reflection of their use in the Middle Ages in both Islamic and Gothic decoration and, after the invention of firearms, in the construction of fortifications.' (Pedoe, p. 68)
In Dürer's book 'Underweysung der Messung' ('Four Books of Measurement', published in 1525) the author gives an exact construction for a regular pentagon (taken from Ptolemy) but here we are playing with another construction of a pentagon, in this case is an equilateral but not equiangular pentagon.
Dürer thought that 'geometry is the right foundation of all painting' and he wanted to be accessible to painters, artists in general and craftsmen. Then he wrote his books in German and the his focus was practical. The construction that we are studying now is a good example because, although it is approximate, it is very accurate and simple to draw.
He draw it using a rusty compass (a compass with fixed radius) that makes the task easier. [Abu'l-Wafa Al-Buzjani (940-998), mathematician and astronomer, was interested in this kind of geometric constructions using a rusty compass and wrote 'A book on those geometric constructions which are necessary for a craftsman'].

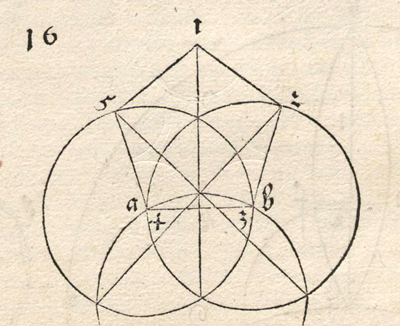
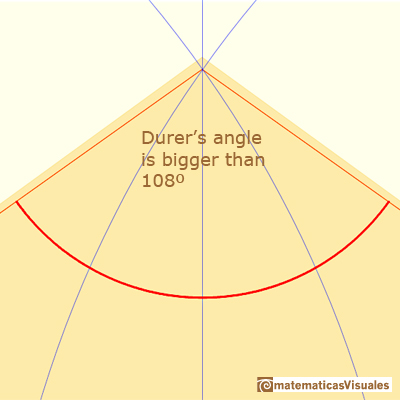
We already know that the five angles of a regular pentagon are 108º. Pedoe wrote that, in Dürer's approximate construction, the angles in the base are 108º21'58'', there are two angles less than 108º and the angle on the top is larger than 109º. This differences would hardly be detectable in a drawing.
We are going to use trigonometry to calculate these angles. For simplicity we can consider that que side length is 1.
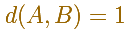
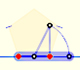
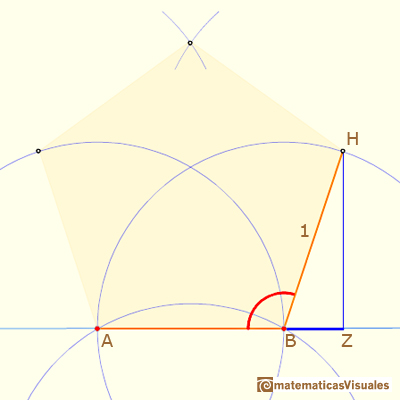
You can start drawing angle ABF:
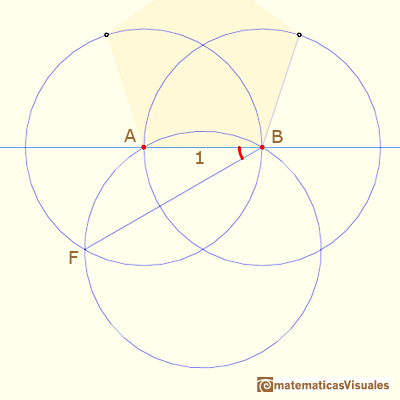
The distance between B and F is twice the height of an equilateral triangle:
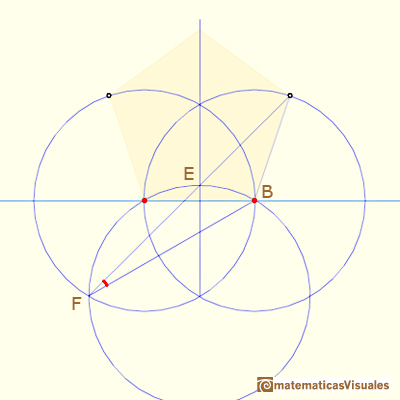
If you remember the properties of the central and inscribed angles in a circle, this is very easy:
Using the Law of Sines we can calculate angle FHB:
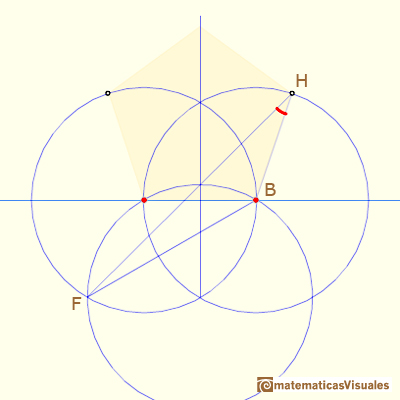
Now we can calculate angle ABH:
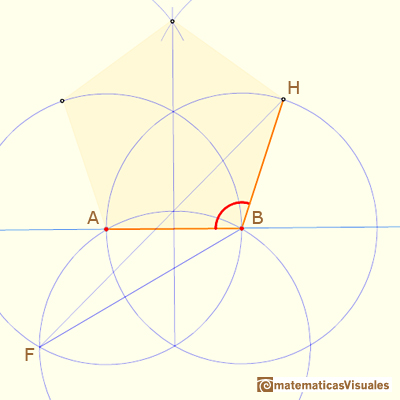
And this angle is bigger than 108º, but the error is very small.
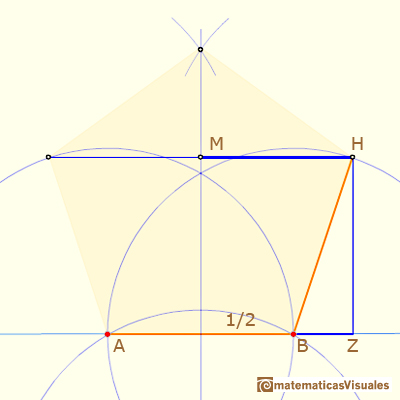
To calculate angles HKI and BHK we can start calculating BZ:
If M is the point in the middle between H and I:
We can calculate angle MHK:
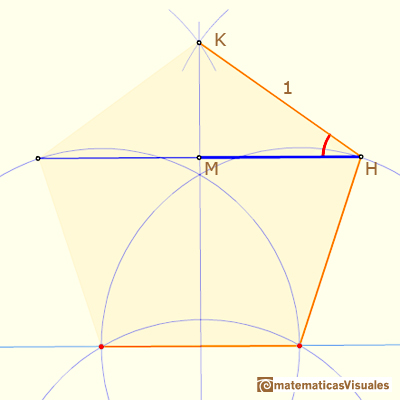
Then, the triangle IHK is an isosceles triangle and it is very easy to calculate angle HKI:
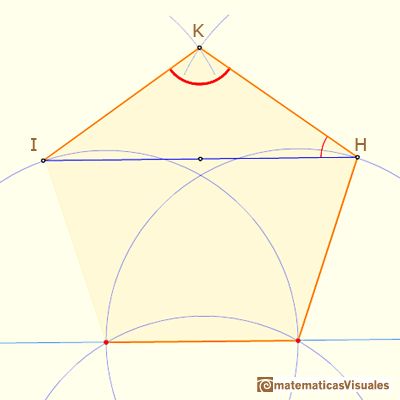
This angle is bigger than 108º.
Finishing our job is now an easy task. Remember that the five angles of a convex pentagon measure three times 180º. We can deduce angle BHK
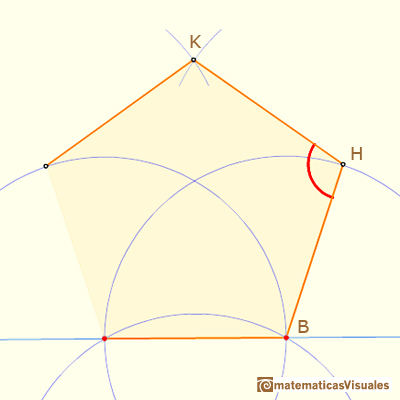
The angle at the top is smaller than 108º.
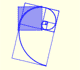
We can play with the zoom and see how accurate is Durer's approximation:
Even zooming you can see that the approximation is very good.
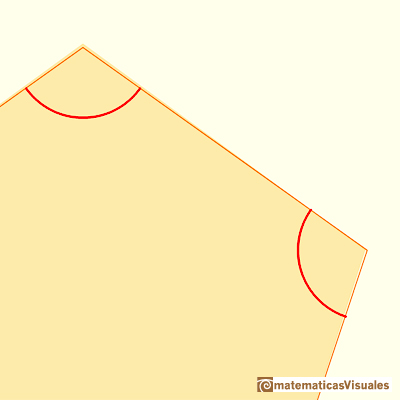
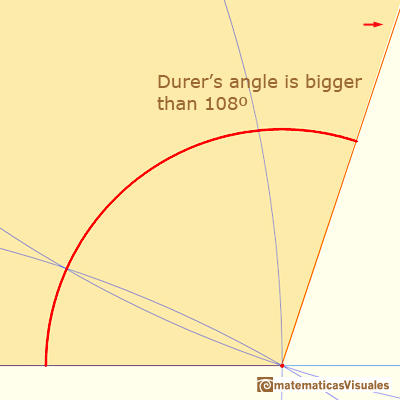
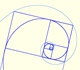
Very close we can see the small error:
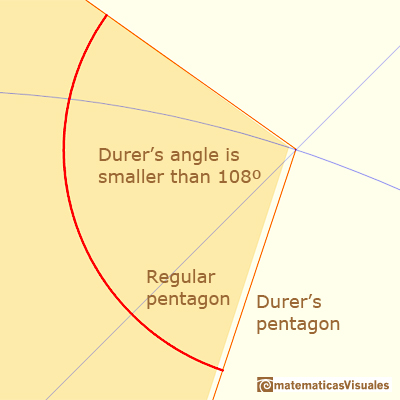
The height of Dürer's pentagon is smaller than the height of a regular pentagon and the angle at the top is bigger:
REFERENCES
 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS