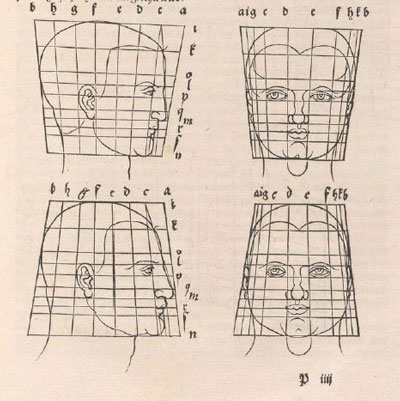
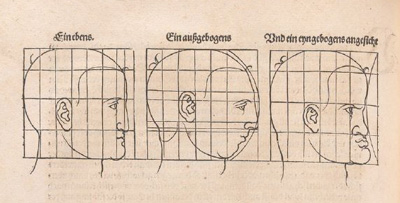
Durer was a painter and also a mathematician. He lived between 1471 and 1528. He was a representative of the German Renaissance.
This was the time of the Reformation. He lived in Nuremberg and traveled to Italy and the Netherlands. He spreads the new techniques of perspective.
He wrote two books in German of particular interest to us. The first is a treatise on
descriptive geometry (Underweysung Underweysung der Messung) with ruler and compass constructions (exact and approximate constructions)
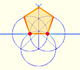
In his book 'Underweysung der Messung' Durer draw a non-regular pentagon with ruler and a fixed compass. It is a simple construction and a very good approximation of a regular pentagon.
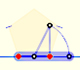
You can draw a regular pentagon given one of its sides constructing the golden ratio with ruler and compass.
In this book you can see the first printed drawings of plane development of polyhedra (plane nets).
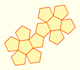
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
The second book is "The four Books of Human Proportions" ("Vier Bücher von Menschlicher Proportionen").
This book has mathematical interest too.
You can browse and download this book on the
Yale University Beinecke Rare Book and Manuscript Library.
In the third book he describes methods
for changing the proportions of the figures, in particular, heads and faces.
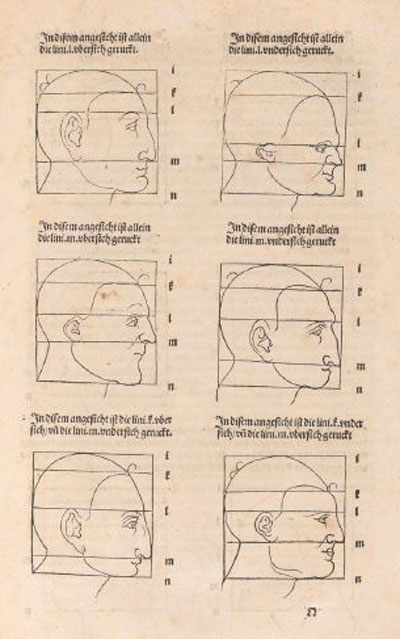
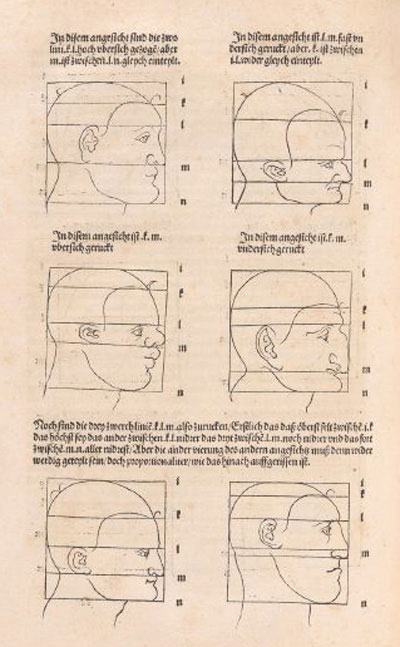
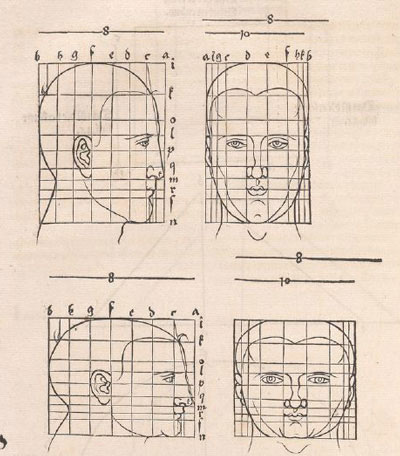
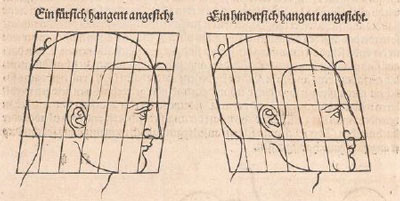
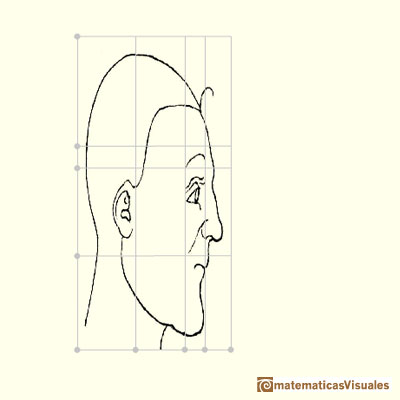
Durer used rectilinear grids in his drawings. Nothing new because this grids were known thousands of years before him and there is archelogical
evidence that the Ancient Egyptians (for example) used rectilinear grids in their drawings.
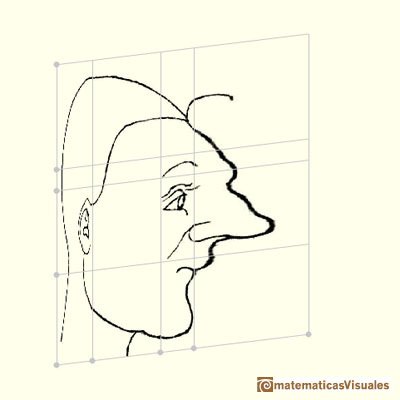
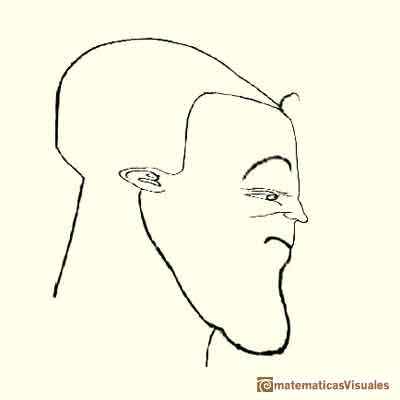
Durer had a new approach: he transforms the grid modifying heads and faces. In some way he used the grid as a primitive "coordinate system".
It is based on geometric transformations of different types.
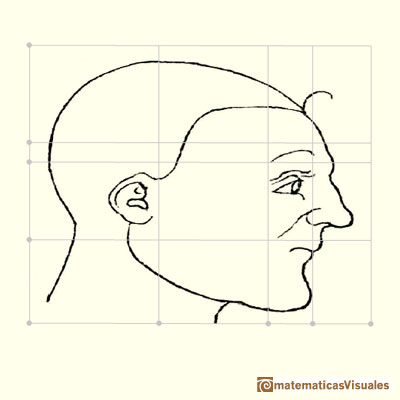
Some of these changes are affine transformations.
Affine transformations include transformations like compression in one direction (stretching).
We can use this kind of transformations to understand Archimedes' method to calculate the area of an ellipse.

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.
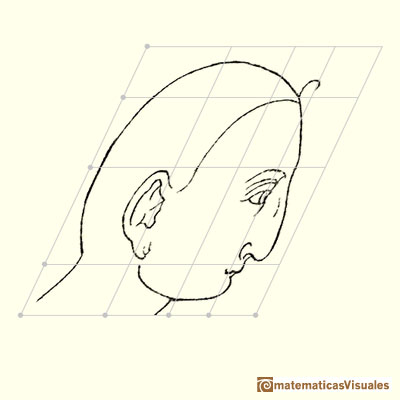
Another affine transformation is a shear which change the angle of the coordinate system.
Affine transformations are linear transformations that conserve parallelism (parallel lines still remain parallel after the transformation).
Durer changed differents areas of the grid differently. We can say that this kind of transformations are "piecewise" affine transformations.
Using this "piecewise" transformations he obtained deformed faces like caricatures, sometimes grotesque.
MORE LINKS

Durer was the first who published in german a method to draw ellipses as cone sections.

Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .
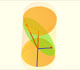
The section of a cylinder by a plane cutting its axis at a single point is an ellipse. A beautiful demonstration uses Dandelin Spheres.

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.

You can draw a regular pentagon given one of its sides constructing the golden ratio with ruler and compass.

The diagonal of a regular pentagon are in golden ratio to its sides and the point of intersection of two diagonals of a regular pentagon are said to divide each other in the golden ratio or 'in extreme and mean ratio'.
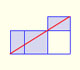
From Euclid's definition of the division of a segment into its extreme and mean ratio we introduce a property of golden rectangles and we deduce the equation and the value of the golden ratio.
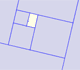
A golden rectangle is made of an square and another golden rectangle.
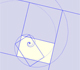
A golden rectangle is made of an square an another golden rectangle. These rectangles are related through an dilative rotation.
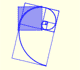
The golden spiral is a good approximation of an equiangular spiral.
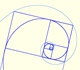
Two equiangular spirals contains all vertices of golden rectangles.

The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron

Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.

The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

The first drawing of a plane net of a regular octahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
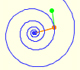
Two transformations of an equiangular spiral with the same general efect.

In an equiangular spiral the angle between the position vector and the tangent is constant.
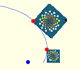
A Dilative Rotation is a combination of a rotation an a dilatation from the same point.





 NEXT
NEXT