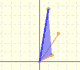
Equiangular Spiral
"For problems involving directions from a fixed origin (or 'pole') O, we often find it convenient to specify a point P by its polar coordinates
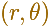
where 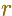 is the
distance OP and
is the
distance OP and
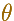 is the angle that the direction OP makes with a given initial line OX, which may be identified with the x-axis of
rectangular Cartesian coordinates. Of course, the point
is the angle that the direction OP makes with a given initial line OX, which may be identified with the x-axis of
rectangular Cartesian coordinates. Of course, the point 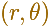 is the same as
is the same as
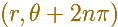 for any integrer n
"
(Coxeter, p.110)
for any integrer n
"
(Coxeter, p.110)
We can use Polar coordinates for describing spirals, for example.
Coxeter introduce the Equiangular Spiral (or 'Logaritmic spiral') as the result of a continuous dilative rotation.
The polar equation of the Equiangular Spiral is
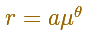
It receives the name of equiangular because the angle between the radius vector and the tangent is constant.
If 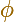 is the angle between the position
vector OP and the tangent at P then (in general, in polar coordinates)
is the angle between the position
vector OP and the tangent at P then (in general, in polar coordinates)
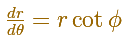
In the Equiangular spiral case, we can write
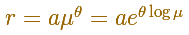
Calculating the derivative
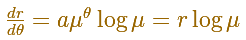
Then
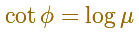
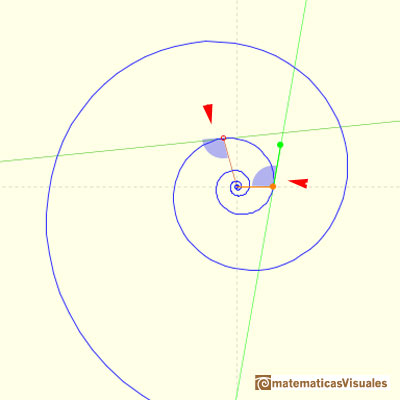
The angle between the position vector OP and the tangent at P is a constant and we can write the Equiangular spiral equation
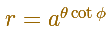
This spiral was called "spiral mirabilis" by Jacob Bernouilli.
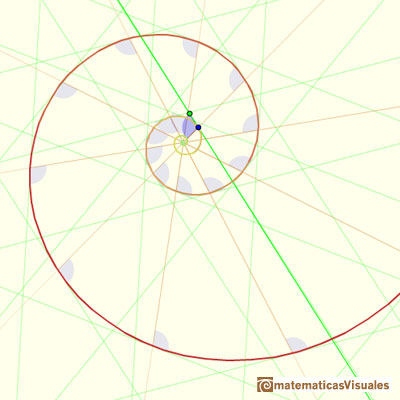
We can see that the angle formed by the radius vector and the tangent is constant.
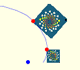
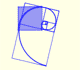
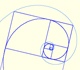
In the next video you can see a particular case: the Golden Equiangular Spiral. This spiral is related with the Golden Rectangle.
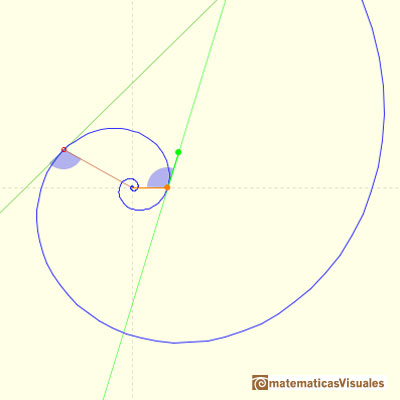
This example is the golden equiangular spiral.
REFERENCES
Coxeter - Introduction to Geometry (John Whiley and sons)
Steinhaus - Mathematical Snapshots.
D'Arcy Thompson - On Growth and Form. (Cambridge University Press)
MORE LINKS
From Euclid's definition of the division of a segment into its extreme and mean ratio we introduce a property of golden rectangles and we deduce the equation and the value of the golden ratio.
A golden rectangle is made of an square an another golden rectangle. These rectangles are related through an dilative rotation.

Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.

The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron













 NEXT
NEXT
 PREVIOUS
PREVIOUS