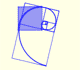
We have already study the golden ratio and several properties of the golden rectangle.
From Euclid's definition of the division of a segment into its extreme and mean ratio we introduce a property of golden rectangles and we deduce the equation and the value of the golden ratio.
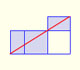
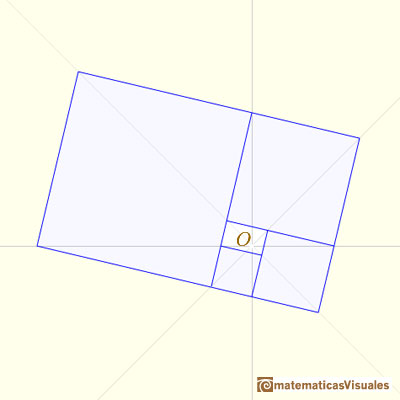
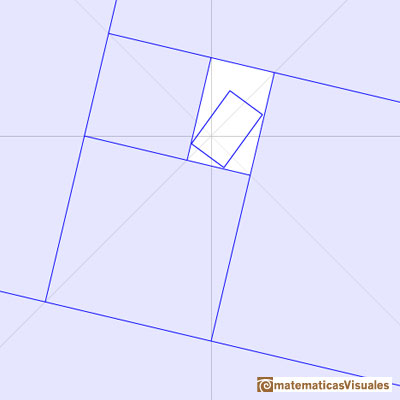
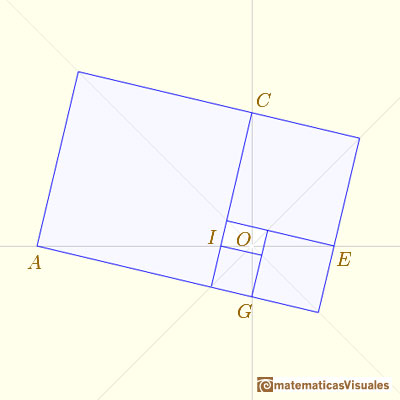
A golden rectangle is made of an square and another golden rectangle.
When we divide a golden rectangle in a square and another golden rectangle this new rectangle is similar
to the initial one. We can repeat this procedure infinitely and we get a geometric sequence of rectangles.
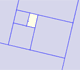
There is a special point O
From one rectangle to get the next one we can consider the transformation that is the product of a dilatation of center O
and a rotation (a negative quater-turn about O)
This transformation is a dilative rotation.
A Dilative Rotation is a combination of a rotation an a dilatation from the same point.
In the next video you can see a continuous dilative rotation:
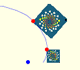
Now we are going to calculate polar coordinates of several points.
The pole is O
Taking OE as the initial line and the length OE as the unit of measurement, so that E is
From E to C the dilative rotation about O has
ratio of magnification 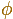 and it is a positive quarter-turn.
and it is a positive quarter-turn.
In general, we can calculate a sequence of points
MORE LINKS

The diagonal of a regular pentagon are in golden ratio to its sides and the point of intersection of two diagonals of a regular pentagon are said to divide each other in the golden ratio or 'in extreme and mean ratio'.
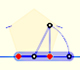
You can draw a regular pentagon given one of its sides constructing the golden ratio with ruler and compass.
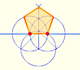
In his book 'Underweysung der Messung' Durer draw a non-regular pentagon with ruler and a fixed compass. It is a simple construction and a very good approximation of a regular pentagon.

From Euclid's definition of the division of a segment into its extreme and mean ratio we introduce a property of golden rectangles and we deduce the equation and the value of the golden ratio.

A Dilative Rotation is a combination of a rotation an a dilatation from the same point.

With three golden rectangles you can build an icosahedron.
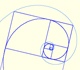
Two equiangular spirals contains all vertices of golden rectangles.

Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
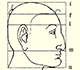
He studied transformations of images, for example, faces.

One eighth of a regular dodecahedon of edge 2 has the same volume as a dodecahedron of edge 1.

The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.
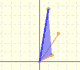
We can see it as a dilatative rotation.
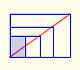
There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.

In an equiangular spiral the angle between the position vector and the tangent is constant.
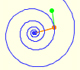
Two transformations of an equiangular spiral with the same general efect.


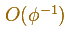
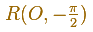
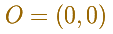
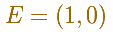
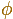 and it is a positive quarter-turn.
and it is a positive quarter-turn.
 NEXT
NEXT
 PREVIOUS
PREVIOUS