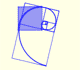
The Golden Rectangle and two equiangular spirals
We can see that some vertices of the golden rectangles of this construction are in an equiangular spiral.
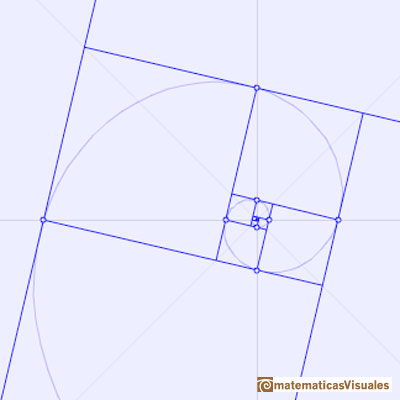
Coxeter ask to prove ("Introduction to Geometry" p 196) that the other vertices also are in another equiangular spiral.
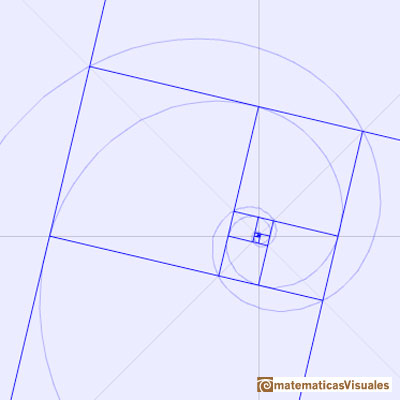
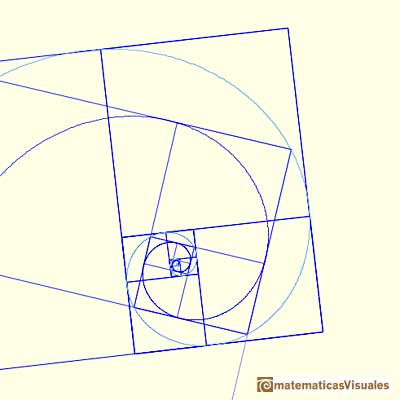
This second golden spiral is homotetic to the initial golden spiral.
This second golden spiral is congruent by rotation to the initial golden spiral.
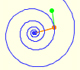
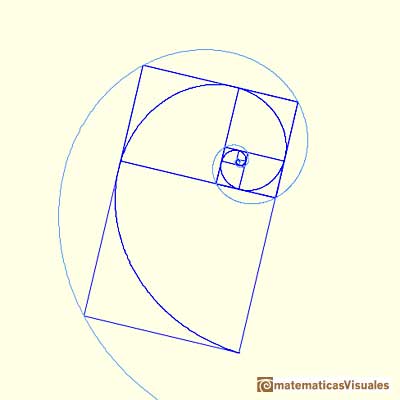
In the next animation we can see the rotation that transforms one spiral into the other.
REFERENCES
Coxeter H. S. M. - Introduction to Geometry (John Whiley and Sons, Second Edition, 1969)
 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS

The diagonal of a regular pentagon are in golden ratio to its sides and the point of intersection of two diagonals of a regular pentagon are said to divide each other in the golden ratio or 'in extreme and mean ratio'.
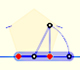
You can draw a regular pentagon given one of its sides constructing the golden ratio with ruler and compass.
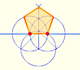
In his book 'Underweysung der Messung' Durer draw a non-regular pentagon with ruler and a fixed compass. It is a simple construction and a very good approximation of a regular pentagon.
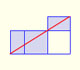
From Euclid's definition of the division of a segment into its extreme and mean ratio we introduce a property of golden rectangles and we deduce the equation and the value of the golden ratio.
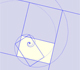
A golden rectangle is made of an square an another golden rectangle. These rectangles are related through an dilative rotation.

Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.