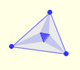The three points of intersection of the adjacent trisectors of the angles of any triangle are the vertices of an equilateral triangle (Morley's triangle)

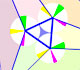Interactive animation about John Conway's beautiful proof of Morley's Theorem

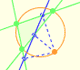Each point in the circle circunscribed to a triangle give us a line (Wallace-Simson line)

Interactive demonstration of the Wallace-Simson line.

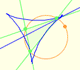The Simson-Wallace lines of a triangle envelops a curve called the Steiner Deltoid.

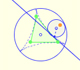Steiner deltoid is a hypocycloid related with the nine point circle of a triangle.

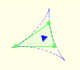Steiner Deltoid and the Morley triangle are related.

Demonstration of Pythagoras Theorem inspired in Euclid.

Dynamic demonstration of the Pythagorean Theorem by Hermann Baravalle.

We can see Pythagoras' Theorem in a tiling. It is a graphic demonstration of Pythagoras' Theorem we can see in some floor made using squares of two different sizes.

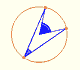Central angle in a circle is twice the angle inscribed in the circle.

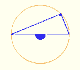Interactive 'Mostation' of the property of central and inscribed angles in a circle. Case I: When the arc is half a circle the inscribed angle is a right angle.

Interactive 'Mostation' of the property of central and inscribed angles in a circle. Case II: When one chord that forms the inscribed angle is a diameter.

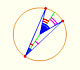Interactive 'Mostation' of the property of central and inscribed angles in a circle. The general case is proved.

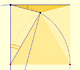Using a ruler and a compass we can draw fifteen degrees angles. These are basic examples of the central and inscribed in a circle angles property.

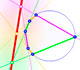If a hexagon is inscribed in a circle, the three pairs of opposite sides meet in collinear points.

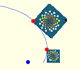A Dilative Rotation is a combination of a rotation an a dilatation from the same point.

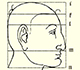He studied transformations of images, for example, faces.

In an equiangular spiral the angle between the position vector and the tangent is constant.

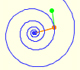Two transformations of an equiangular spiral with the same general efect.

There are infinitely many equiangular spirals through two given points.

The diagonal of a regular pentagon are in golden ratio to its sides and the point of intersection of two diagonals of a regular pentagon are said to divide each other in the golden ratio or 'in extreme and mean ratio'.

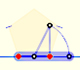You can draw a regular pentagon given one of its sides constructing the golden ratio with ruler and compass.

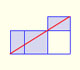From Euclid's definition of the division of a segment into its extreme and mean ratio we introduce a property of golden rectangles and we deduce the equation and the value of the golden ratio.

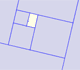A golden rectangle is made of an square and another golden rectangle.

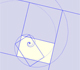A golden rectangle is made of an square an another golden rectangle. These rectangles are related through an dilative rotation.

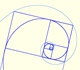Two equiangular spirals contains all vertices of golden rectangles.

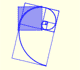The golden spiral is a good approximation of an equiangular spiral.

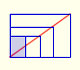There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.

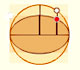Transforming a circle we can get an ellipse (as Archimedes did to calculate its area). From the equation of a circle we can deduce the equation of an ellipse.

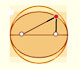Every ellipse has two foci and if we add the distance between a point on the ellipse and these two foci we get a constant.

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.

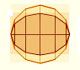In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.

An Ellipsograph is a mechanical device used for drawing ellipses.

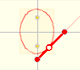If a straight-line segment is moved in such a way that its extremities travel on two mutually perpendicular straight lines then the midpoint traces out a circle; every other point of the line traces out an ellipse.

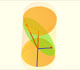The section of a cylinder by a plane cutting its axis at a single point is an ellipse. A beautiful demonstration uses Dandelin Spheres.

Durer was the first who published in german a method to draw ellipses as cone sections.

Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .

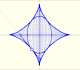The Astroid is the envelope of a segment of constant length moving with its ends upon two perpendicular lines. It is also the envelope of a family of ellipses, the sum of whose axes is constant.

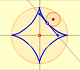The Astroid is a particular case of a family of curves called hypocycloids.

The volume of a tetrahedron is one third of the prism that contains it.

Special sections of a tetrahedron are rectangles (and even squares). We can calculate the area of these cross-sections.

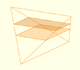In his article 'Two Surprising Theorems on Cavalieri Congruence' Howard Eves describes an interesting tetrahedron. In this page we calculate its cross-section areas and its volume.

Howard Eves's tetrahedron is Cavalieri congruent with a given sphere. You can see that corresponding sections have the same area. Then the volumen of the sphere is the same as the volume of the tetrahedron. And we know how to calculate this volumen.

Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.

One eighth of a regular dodecahedon of edge 2 has the same volume as a dodecahedron of edge 1.

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.

The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron

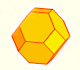The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.

These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.

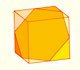We can cut in half a cube by a plane and get a section that is a regular hexagon. Using eight of this pieces we can made a truncated octahedron.

Using eight half cubes we can make a truncated octahedron. The cube tesselate the space an so do the truncated octahedron. We can calculate the volume of a truncated octahedron.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.

The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.

The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.

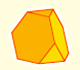The truncated tetrahedron is an Archimedean solid made by 4 triangles and 4 hexagons.

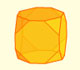When you truncate a cube you get a truncated cube and a cuboctahedron. If you truncate an octahedron you get a truncated octahedron and a cuboctahedron.

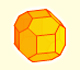You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.

A Cube can be inscribed in a Dodecahedron. A Dodecahedron can be seen as a cube with six 'roofs'. You can fold a dodecahedron into a cube.

If you fold the six roofs of a regular dodecahedron into a cube there is an empty space. This space can be filled with an irregular dodecahedron composed of identical irregular pentagons (a kind of pyritohedron).

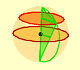We want to calculate the surface area of sections of a sphere using the Pythagorean Theorem. We also study the relation with the Geometric Mean and the Right Triangle Altitude Theorem.

We study a kind of polyhedra inscribed in a sphere, in particular the Campanus' sphere that was very popular during the Renaissance.

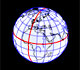Basic world map in a sphere. Latitude and longitude

This perpective projection is area-preserving. If we know the surface area of a sphere we can deduce the volume of a sphere, as Archimedes did.

Humankind has always been fascinated by how bees build their honeycombs. Kepler related honeycombs with a polyhedron called Rhombic Dodecahedron.

We want to close a hexagonal prism as bees do, using three rhombi. Then, which is the shape of these three rhombi that closes the prism with the minimum surface area?.

Adding six pyramids to a cube you can build new polyhedra with twenty four triangular faces. For specific pyramids you get a Rhombic Dodecahedron that has twelve rhombic faces.

You can build a Rhombic Dodecahedron adding six pyramids to a cube. This fact has several interesting consequences.

The Rhombic Dodecahedron fills the space without gaps.

A chain of six pyramids can be turned inwards to form a cube or turned outwards, placed over another cube to form the rhombic dodecahedron.

Kepler understood that the Rhombic Dodecahedron is related with the optimal sphere packing. If a precise structure of balls is squeezed we get rhombic dodecahedra.

The obtuse angle of a rhombic face of a Rhombic Dodecahedron is known as Maraldi angle. We need only basic trigonometry to calculate it.

Using a basic knowledge about the Rhombic Dodecahedron, it is easy to calculate the density of the optimal packing of spheres.

Tetraxis is a wonderful puzzle designed by Jane and John Kostick. We study some properties of this puzzle and its relations with the rhombic dodecahedron. We can build this puzzle using cardboard and magnets or using a 3D printer.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the rhombicuboctahedron.

This polyhedron is also called Elongated Square Gyrobicupola. It is similar to the Rhombicuboctahedron but it is less symmetric.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the augmented rhombicuboctahedron.

We can see the interior of the augmented rhombicuboctahedron. Luca Pacioli wrote that you 'can see the interior only with your imagination'.

Starting with a Rhombicubotahedron we can add pyramids over each face. The we get a beautiful polyhedron that it is like a star.

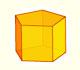We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.

Plane nets of prisms with a regular base with different side number cut by an oblique plane.

We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.

We study different cylinders cut by an oblique plane. The section that we get is an ellipse.

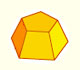Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.

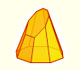Plane net of pyramids cut by an oblique plane.

Plane developments of cones and conical frustum. How to calculate the lateral surface area.

Plane developments of cones cut by an oblique plane. The section is an ellipse.

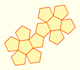The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

The first drawing of a plane net of a regular octahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Using cardboard you can draw plane nets and build polyhedra.

Using cardboard you can build beautiful polyhedra cutting polygons and glue them toghether. This is a very simple and effective technique. You can download several templates. Then print, cut and glue: very easy!

A very simple technique to build complex and colorful polyhedra.

Simple technique to build polyhedra gluing discs made of cardboard or paper.

Italian designer Bruno Munari conceived 'Acona Biconbi' as a work of sculpture. It is also a beautiful game to play with colors and shapes.

With three golden rectangles you can build an icosahedron.

Modular Origami is a nice technique to build polyhedra.

Examples of polyhedra built using tubes.

Examples of polyhedra built using Zome.

Examples of polyhedra built using tensegrity.

Material for a session about polyhedra (Zaragoza, 9th May 2014). Simple techniques to build polyhedra like the tetrahedron, octahedron, the cuboctahedron and the rhombic dodecahedron. We can build a box that is a rhombic dodecahedron.

Material for a session about polyhedra (Zaragoza, 7th November 2014). We study the octahedron and the tetrahedron and their volumes. The truncated octahedron helps us to this task. We build a cubic box with cardboard and an origami tetrahedron.

Material for a session about polyhedra (Zaragoza, 23rd Octuber 2015) . Building a cube with cardboard and an origami octahedron.

Material for a session about polyhedra (Zaragoza, 21st October 2016). Instructions to build several geometric bodies.

Material for a session about polyhedra (Zaragoza, el 20th October 2017). Instruction to build an origami tetrahedron.

Microarquitectura is a construction game developed by Sara San Gregorio. You can play and build a lot of structures modelled on polyhedra.

Building tetraedra using 3d printing. The tetrahedron is a self-dual polyhedron. The center of a tetrahedron.

Building cubes and octahedra using 3d printing. Cube and Octahedron are dual polyhedra.