A pyramid is a polyhedron with a polygonal face (known as the base) and the other faces are triangles meeting at a common point (the apex of the pyramid). These faces (lateral faces) are triangles.

One particular case is when the base is inscribed in a circle. In the first mathlet we can play with pyramids that have a regular polygon as a base. If the apex is above the center of this circle, then we can say that the pyramid is a right pyramid. A regular pyramid is a right pyramid whose base is a regular polygon.

The main interest of this page is to see how a pyramid can be developed into a plane.

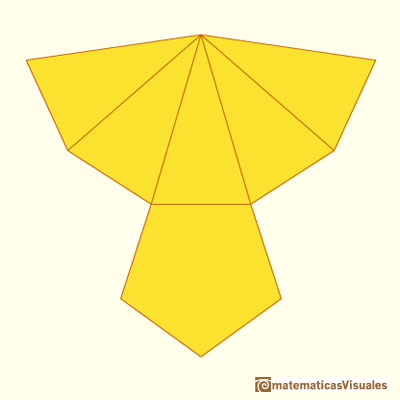
Plane development or net of a pentagonal pyramid:

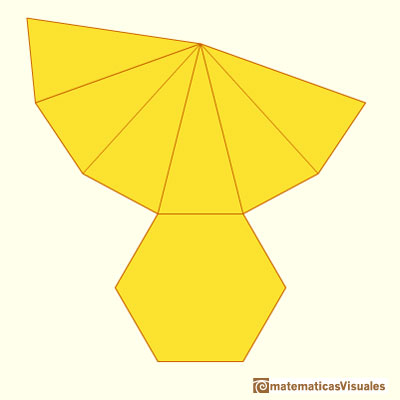
Another example, the net of an hexagonal pyramid:

To calculate the lateral surface area of a pyramid we need the slant height. The slant height of a pyramid if the distance between the apex and the center of a side of the base. It is the altitude of a lateral face. There is a relation between the slant height and the height of a pyramid (Pythagorean theorem).

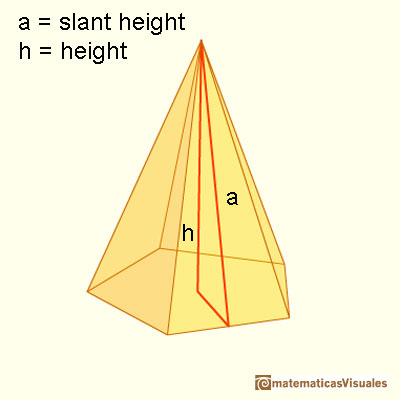
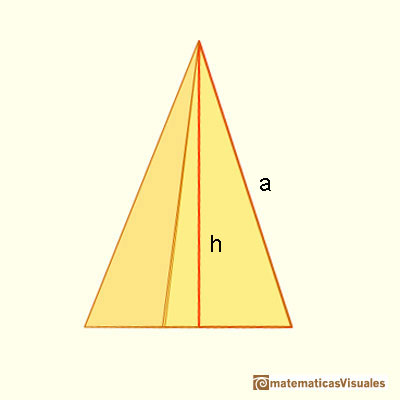
We are going to calculate the lateral surface area of a pyramid. If P is the base perimeter, the formula for the lateral surface area of a pyramid (lateral faces are triangles) is like the formula for the area of a triangle:

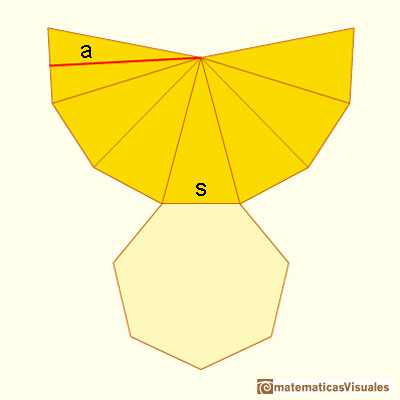
When we study the lateral surface area of a cone, the formula will be similar (as Kepler and the area of a circle.)

The most regular pyramid is a tetrahedron.It is a platonic solid made by four equilateral triangles. Then a tetrahedron is a particular case of a triangular pyramid.

And this is the plane net of a tetrahedron:

When we cut a pyramid by a plane parallel to the base we get a pyramidal frustum (or a truncated pyramid).

For example, this is an hexagonal frustum:

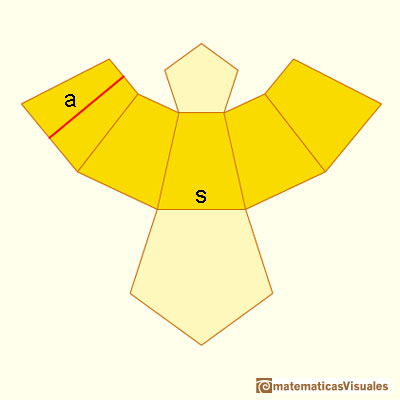
And this is its plane net:

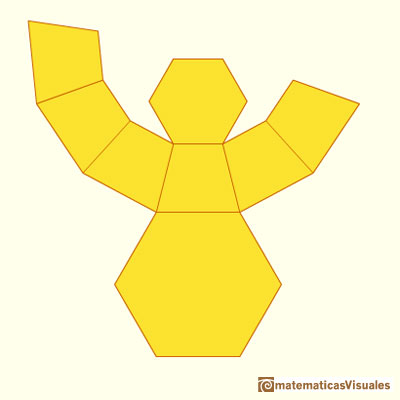
Another example:

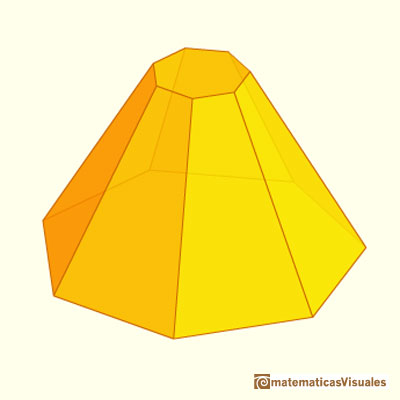
As before, we need the slant height to calculate the lateral surface area of a frustum:

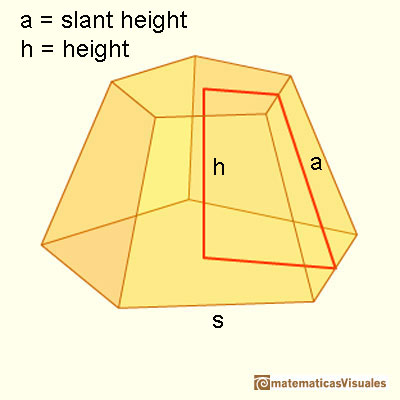
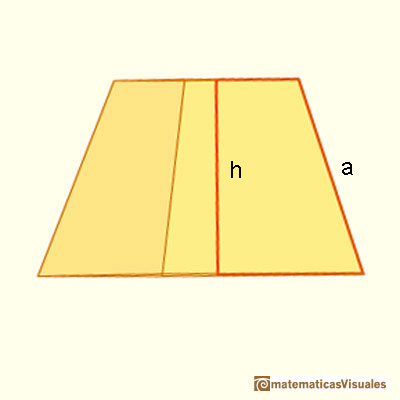
If P is the bottom base perimeter and p the top base perimeter, the formula for the lateral surface area is like the formula for the area of a trapezoid (lateral faces are congruent trapezoids):

In the examples above bases were regular polygons. But we can consider pyramids whose bases are not regular polygons. In the next mathlet, bases are non-regular polygons (although they are inscribed in a circle and they are convex polygons). Each time we change the number of sides of the base a new prism is generated with sides randomly drawn:

MORE LINKS

Plane developments of geometric bodies (7): Cone and conical frustrum

Plane developments of cones and conical frustum. How to calculate the lateral surface area.

Plane developments of geometric bodies (8): Cones cut by an oblique plane

Plane developments of cones cut by an oblique plane. The section is an ellipse.

Plane developments of geometric bodies (3): Cylinders

We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.

Plane developments of geometric bodies (2): Prisms cut by an oblique plane

Plane nets of prisms with a regular base with different side number cut by an oblique plane.

Plane developments of geometric bodies (1): Nets of prisms

We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.

Plane developments of geometric bodies: Dodecahedron

The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Plane developments of geometric bodies: Octahedron

The first drawing of a plane net of a regular octahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Plane developments of geometric bodies: Tetrahedron

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

The volume of the tetrahedron

The volume of a tetrahedron is one third of the prism that contains it.

Plane developments of geometric bodies: Tetrahedron

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Volume of an octahedron

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.

The icosahedron and its volume

The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron

Regular dodecahedron

Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.

Chamfered Cube

You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.

Resources: How to build polyhedra using paper and rubber bands

A very simple technique to build complex and colorful polyhedra.