|
|
|
Pyramids cut by an oblique plane and their nets
En plane developments of geometric bodies (5): Pyramid and pyramidal frustrum we can study pyramids, pyramids cut by a plane parallel to the base and their developments into a plane net. In this page we are going to see how a pyramid cut by an oblique plane can be developed into a plane net.
We have already seen similar cases in plane developments of geometric bodies (2): Prisms cut by an oblique plane and in plane developments of geometric bodies (4): Cylinders cut by an oblique plane.
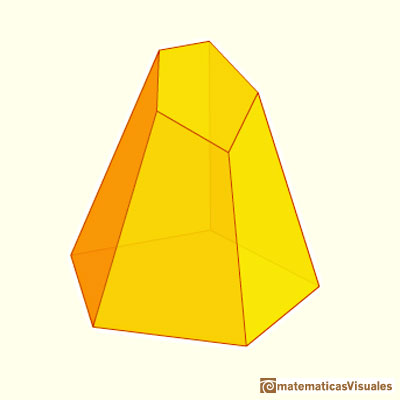
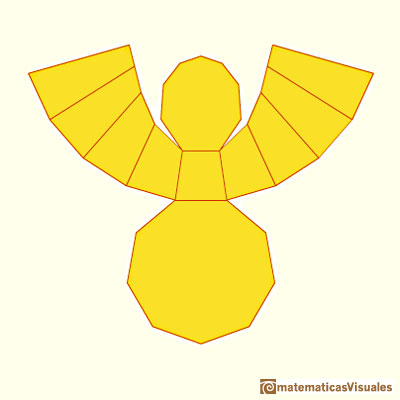
This in another example:
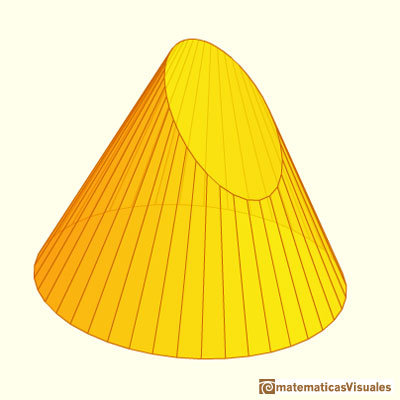
When the pyramid has a lot of faces it is, in some way, like a cone and the oblique section resembles an ellipse:
NEXT
Plane developments of cones and conical frustum. How to calculate the lateral surface area.
PREVIOUS
Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.
MORE LINKS
Plane developments of cones cut by an oblique plane. The section is an ellipse.
We study different cylinders cut by an oblique plane. The section that we get is an ellipse.
We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.
Plane nets of prisms with a regular base with different side number cut by an oblique plane.
We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
The first drawing of a plane net of a regular octahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.
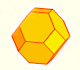
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
The volume of a tetrahedron is one third of the prism that contains it.
The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
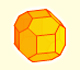
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.
A very simple technique to build complex and colorful polyhedra.