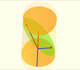
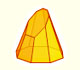
Cone cut by an oblique plane
A cone can be cut by an oblique plane.
The main interest of this page is to see how a cone cut by an oblique plane can be developed into a plane.



This in another example:

 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS

Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .
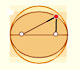
Every ellipse has two foci and if we add the distance between a point on the ellipse and these two foci we get a constant.
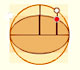
Transforming a circle we can get an ellipse (as Archimedes did to calculate its area). From the equation of a circle we can deduce the equation of an ellipse.

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.
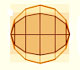
In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.
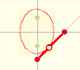
If a straight-line segment is moved in such a way that its extremities travel on two mutually perpendicular straight lines then the midpoint traces out a circle; every other point of the line traces out an ellipse.

We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.