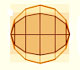
We had already study plane sections of a cylinder.
We suspect that that the intersection of a plane and a cylinder (not parallel to its axis) is an ellipse.

In this page we are going to prove that result using one idea due to Germinal Pierre Dandelin (1794-1847). Dandelin was a Belgian mathematician and military engineer.
We know a lot of things about ellipses. An ellipse is commonly defined as the locus of points P such that the sum of the distances from P to two fixed points F1, F2 (called foci) are constant. We are going to use this definition later.
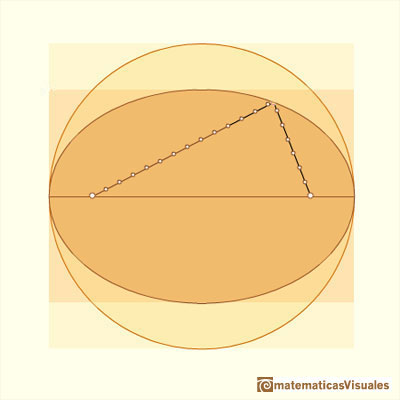
We know how to calculate the area of the ellipse:

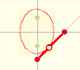
Even we can build mechanical devices to draw ellipses:
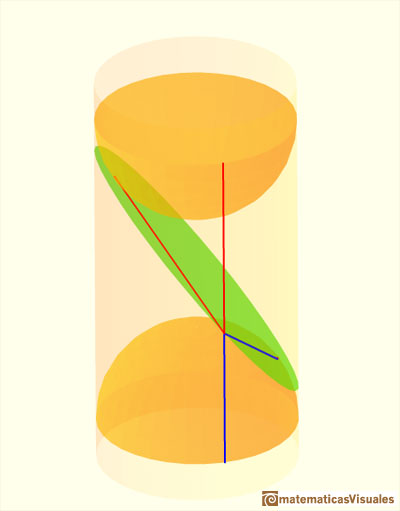
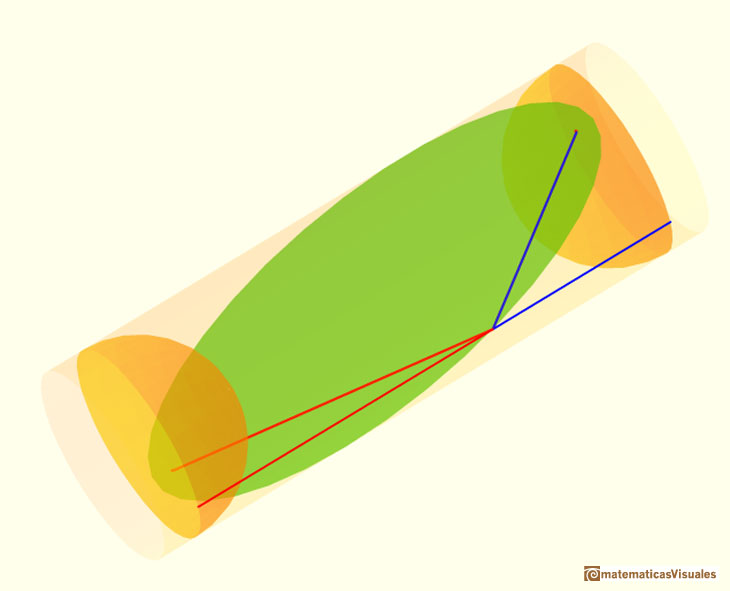
Dandelin's idea is to consider two spheres inscribed in the cylinder and tangent to the plane that intersect the cylinder. Each of these spheres is tangent to the cylinder in a circle. These circles are parallel and the distance between those circles along any generating line of the cylinder is constant.
These spheres are called Dandelin's spheres.
We shall prove that the points of tangency are the foci of the ellipse.
Playing with the interactive application we can change the distance between the spheres, move the point on the curve and rotate the cylinder.
We are going to follow Hilbert and Cohn-Vossen's book 'Geometry and the Imagination':
"A circular cylinder intersects every plane at right angles to its axis in a circle. A plane not at right angles to the axis nor parallel to it intersects the cylinder in a curve that looks like an ellipse. We shall prove this curve really is an ellipse. To this end, we take a sphere that just fits into the cylinder, and move it within the cylinder until it touches the intersecting plane (Fig. 9)."
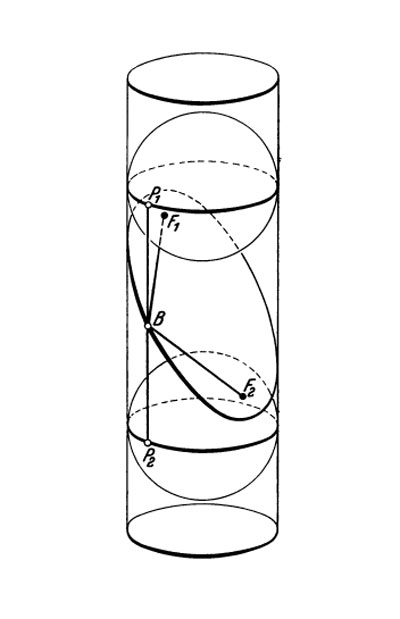
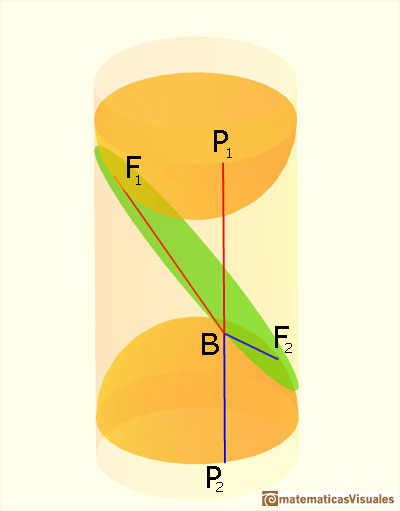

"We then take another such sphere and do the same thing with it ont the other side of the plane. The spheres touch the cylinder in two circles and touch the intersecting plane at two points, F1 and F2. Let B be any point on the curve of intersection of the plane with the cylinder. Consider the straight line through B lying on the cylinder (i.e. parallel to the axis). It meets the circle of contact of the spheres at two points P1 and P2. BF1 and BP1 are tangents to a fixed sphere through a fixed point B, and all such tangents must be equal, because of the rotational symmetry of the sphere. Thus BF1=BP1; and similarly BF2=BP2. It follows that
But by the rotational symmetry of our figure, the distance P1P2 is independent of the point B on the curve. Therefore BF1+BF2 is constant for all points B of the section; i.e. the curve is an ellipse with foci at F1 and F2."
"The fact that we have just proved can also be formulated in terms of the theory of projections as follows: The shadow that a circle throws onto an oblique plane is an ellipse if the light rays are perpendicular to the plane of the circle." (Hilbert and Cohn-Vossen. Geometry and the Imagination)
A particular case: the circle (the two foci are the same point that we call the certer of the circle).






More general, the intersection of a plane and a cone is a conic section (ellipse, hyperbola, parabola).
REFERENCES
 PREVIOUS
PREVIOUS
MORE LINKS




















 NEXT
NEXT