In his book 'On Conoids and Spheroids', Archimedes computed the area of an ellipse (Proposition 4).

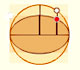
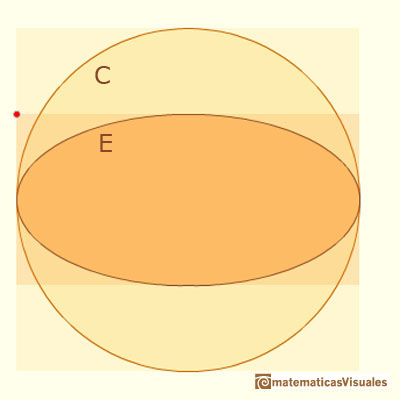
When we shrink vertically a circle we get an ellipse. An ellipse has a major and a minor semi-axis.

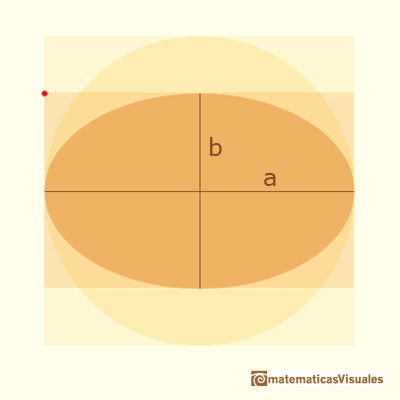
The formula for the area of an ellipse is a beautiful generalization of the area of a circle. The area of an ellipse with major and minor semi-axes a and b is:

First we are going to deduce this formula using an intuitive approach. Archimedes had a clear distinction between his 'Method' of discovering results and a theorem rigurous proof. We can see a good example of Archimedes' 'Method' for discovering in Archimedes: Area of a Parabolic Segment.

After that, we are going to explain how Archimedes demonstrated the result.

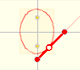
The circle of radius a, circunscribed about the ellipse is called its auxiliary circle. If we shrink (vertically) the circle we get an ellipse. Given a point m in the ellipse it satisfy the relation:

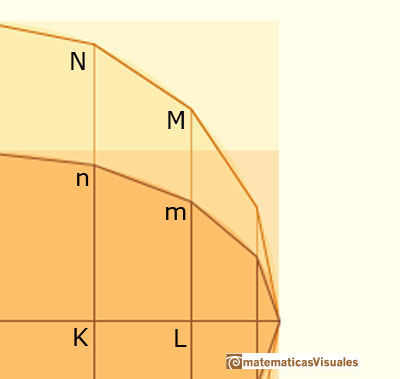
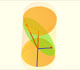
Archimedes considered some polygons inscribed in the ellipse and in the auxiliary circle. These polygons having its number of sides equals to a multiple of 4 and with opposite ends of the horizontal diameter as vertices.

The polygon, P', inscribed in the circle is a regular polygon and P is the polygon inscribed in the ellipse E whose vertices are the intersections with E of the perpendiculars from the vertices of P' to the horizontal axis of E. We can consider these polygons as unions of triangles and trapezoids. Because of the shrinking we have the relation:

Then the two areas of the two polygons P and P' are in the same relation:

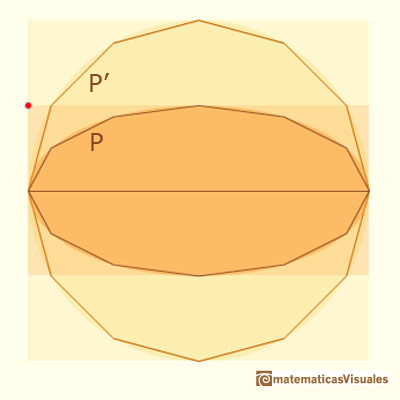
But these polygons can have as much sides as we want and they can be so similar to the circle and the ellipse as we want, then we are going to agree that: (they exhaust the circle and the ellipse)

Then we get the formula for the area of an ellipse:

If our intuituion is correct, this is the formula for the area of an ellipse. Using the zoom over the mathlet we can see that the approximation is very good but that the polygon never fills the ellipse nor the circle.

This is a nice approach but Archimedes needed a logical and rigorous proof. His proof is not an example of the use of Eudoxus's exhaustion tecnique with inscribed and excribed polygons but it is a good example of the typical use that Archimedes made of a double 'reductio ad absurdum'.

MORE LINKS

Equation of an ellipse

Transforming a circle we can get an ellipse (as Archimedes did to calculate its area). From the equation of a circle we can deduce the equation of an ellipse.

Ellipsograph or Trammel of Archimedes

An Ellipsograph is a mechanical device used for drawing ellipses.

Ellipsograph or Trammel of Archimedes (2)

If a straight-line segment is moved in such a way that its extremities travel on two mutually perpendicular straight lines then the midpoint traces out a circle; every other point of the line traces out an ellipse.

Ellipses as sections of cylinders: Dandelin Spheres

The section of a cylinder by a plane cutting its axis at a single point is an ellipse. A beautiful demonstration uses Dandelin Spheres.

Albert Durer and ellipses: cone sections.

Durer was the first who published in german a method to draw ellipses as cone sections.

Albert Durer and ellipses: Symmetry of ellipses.

Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .

The Astroid as envelope of segments and ellipses

The Astroid is the envelope of a segment of constant length moving with its ends upon two perpendicular lines. It is also the envelope of a family of ellipses, the sum of whose axes is constant.

The Astroid is a hypocyclioid

The Astroid is a particular case of a family of curves called hypocycloids.

Plane developments of geometric bodies (4): Cylinders cut by an oblique plane

We study different cylinders cut by an oblique plane. The section that we get is an ellipse.

Plane developments of geometric bodies (8): Cones cut by an oblique plane

Plane developments of cones cut by an oblique plane. The section is an ellipse.

Archimedes' Method to calculate the area of a parabolic segment

Archimedes show us in 'The Method' how to use the lever law to discover the area of a parabolic segment.

Kepler: The Area of a Circle

Kepler used an intuitive infinitesimal approach to calculate the area of a circle.

Durer and transformations

He studied transformations of images, for example, faces.

The Complex Cosine Function

The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.