Knowing the result, Archimedes considered a secondary circle with the same area than the ellipse.

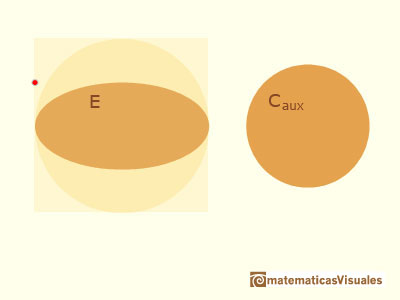
The radius of this circle is:

Archimedes wanted to probe that the area of the ellipse is equal to the area of this secondary circle

Archimedes considered an auxiliary polygon similar to P', the polygon inscribed in the auxiliary circle C'.

The relation between the areas of these two similar polygons is:

Archimedes estarted his double 'reductio ad absurdum'.

If posible, let the secundary circle greater than the ellipse.

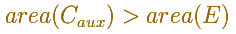
"We can then inscribe in the secundary circle an equilateral polygon of 4n sides such that its area is greater than that of the ellipse. [cf. On the Sphere and Cylinder, I. 6.]" (Archimedes)

Then

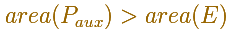
Then we can consider a similar polygon in the auxiliary circle and the corresponding polygon in the ellipse.

"Supose that P' denotes the area of the polygon inscribed in the auxiliary circle, and P that of the polygon inscribed in the ellipse." (Archimedes)

We already know that

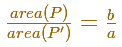
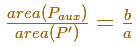
Then

"But this is imposible, because the later polygon is by hypothesis greater than the ellipse, and a fortiory greater than P.

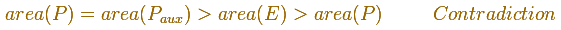
Hence the secondary circle is not greater than the ellipse." (Archimedes)

If posible, let the secundary circle be less than the ellipse.

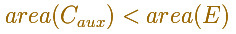
In this case we inscribe in the ellipse a polygon P with 4n equal sides such that

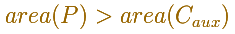
Archimedes consider polygon P' inscribed to the auxiliary circle and a similar polygon inscribed in the secondary circle.

As before

which is imposible

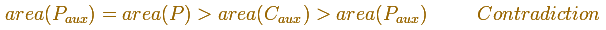
This completes the double reductio ad absurdum proof.

"Hence the secondary circle, being neither greater nor less than the ellipse, si equal to it; and the required result follows."(Archimedes)

"In esence, Archimedes has simply given a rigorous exhaustion proof of the intuitively evident fact that the area of the ellipse is b/a times the area of its auxiliary circle, corresponding to the observation that the circle is transformed into the ellipse by shrinking its vertical dimension by the factor b/a" (C. H. Edwards)

MORE LINKS

Plane developments of geometric bodies (8): Cones cut by an oblique plane

Plane developments of cones cut by an oblique plane. The section is an ellipse.

Equation of an ellipse

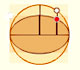
Transforming a circle we can get an ellipse (as Archimedes did to calculate its area). From the equation of a circle we can deduce the equation of an ellipse.

Ellipse and its foci

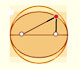
Every ellipse has two foci and if we add the distance between a point on the ellipse and these two foci we get a constant.

Ellipsograph or Trammel of Archimedes

An Ellipsograph is a mechanical device used for drawing ellipses.

Ellipsograph or Trammel of Archimedes (2)

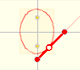
If a straight-line segment is moved in such a way that its extremities travel on two mutually perpendicular straight lines then the midpoint traces out a circle; every other point of the line traces out an ellipse.

Ellipses as sections of cylinders: Dandelin Spheres

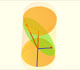
The section of a cylinder by a plane cutting its axis at a single point is an ellipse. A beautiful demonstration uses Dandelin Spheres.

Albert Durer and ellipses: cone sections.

Durer was the first who published in german a method to draw ellipses as cone sections.

Albert Durer and ellipses: Symmetry of ellipses.

Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .

The Astroid as envelope of segments and ellipses

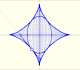
The Astroid is the envelope of a segment of constant length moving with its ends upon two perpendicular lines. It is also the envelope of a family of ellipses, the sum of whose axes is constant.

The Astroid is a hypocyclioid

The Astroid is a particular case of a family of curves called hypocycloids.

Archimedes' Method to calculate the area of a parabolic segment

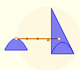
Archimedes show us in 'The Method' how to use the lever law to discover the area of a parabolic segment.

Kepler: The Area of a Circle

Kepler used an intuitive infinitesimal approach to calculate the area of a circle.

Durer and transformations

He studied transformations of images, for example, faces.

The Complex Cosine Function

The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.