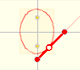
In this page we study an instrument for drawing ellipses. It is called "Ellipsograph" or "Trammel of Archimedes".
The word 'trammel' in this context has a meaning of restrain, something impeding activity, a constraint that restrics freedom. The origin of this word is
related with a net to catch fish.
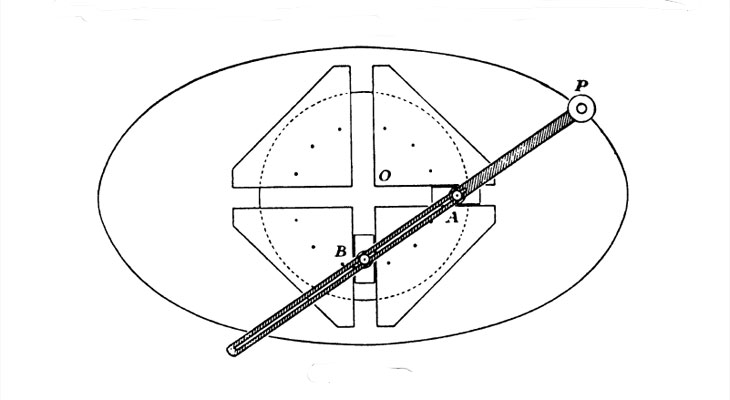
We can see a classical representation of this tool in Cundy and Rollet's book 'Mathematical Models'.
Classical representation of this tool in Cundy and Rollet's book 'Mathematical Models'.
"Four triangular cheek-pieces are bolted firmly to a base-plate which rests on the paper. They form the walls of two slots at right angles
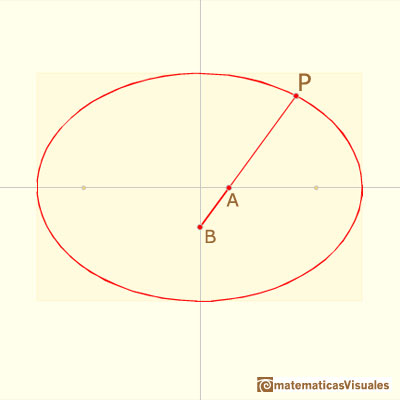
in which the sliders A and B can run. PAB is a slotted arm which can be screwed to the sliders at A and B in such a way that it is free to
rotate on the slider, but not to slip along the slot AB. The sliders must be longer than the width of the slots at O to ensure
free travel across the opening.(...) By adjusting the screws, ellipses of different sizes can be drawn by a tracing point at P." (Cundy and Rollet, p. 240)
We can say that the two sliders are 'trammelled' or confined by the two slots and the rod.
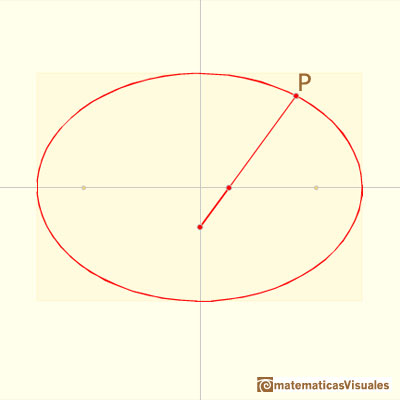
We want to prove that point P draws an ellipse.
Some properties of ellipses have been studied in other pages of matemáticasVisuales.
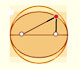
Every ellipse has two foci and if we add the distance between a point on the ellipse and these two foci we get a constant.
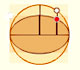
Transforming a circle we can get an ellipse (as Archimedes did to calculate its area). From the equation of a circle we can deduce the equation of an ellipse.

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.
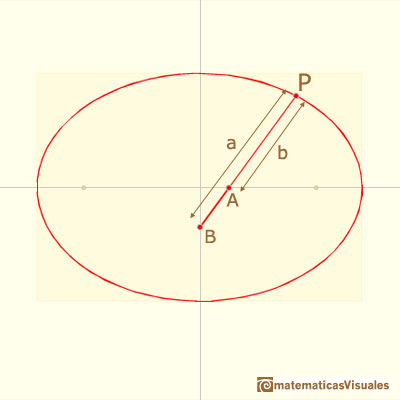
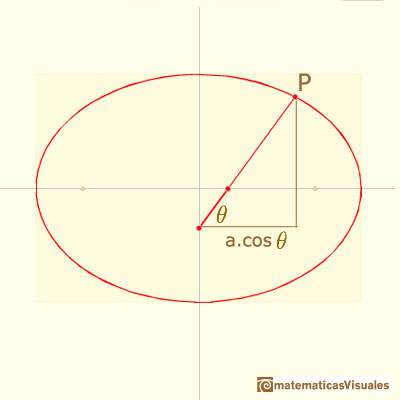
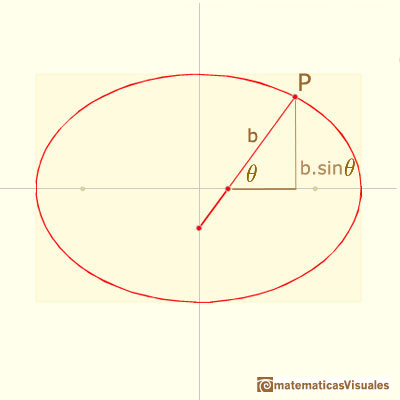
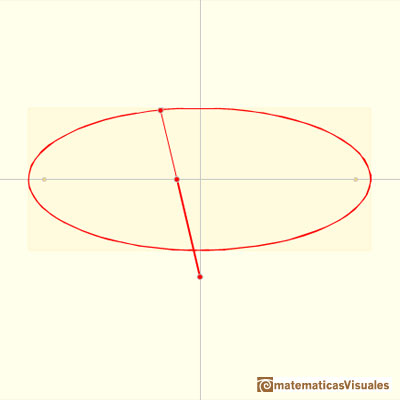
To calculate coordinates of point P we are going to use this notation and trigonometry:
Then the X coordinate of point P is:
And the Y coordinate is:
Then, the coordinates of point P are:
These coordinates verify the implicit formula of the ellipse:
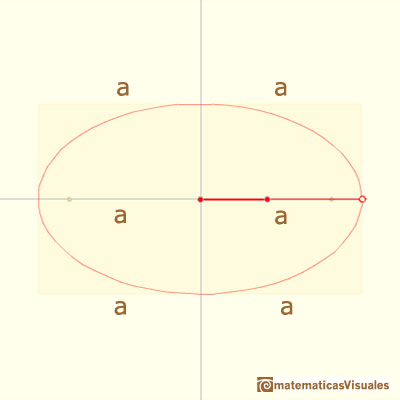
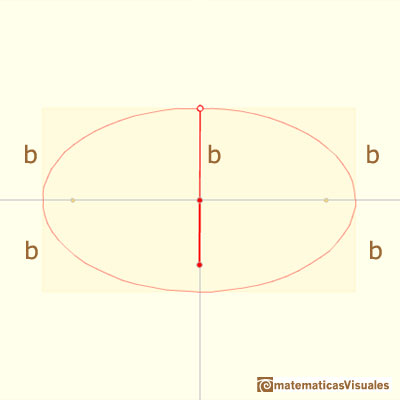
The two semi-axis of the ellipse are a and b, it is to say, the distances between the end of the rod and the two pivoted points:
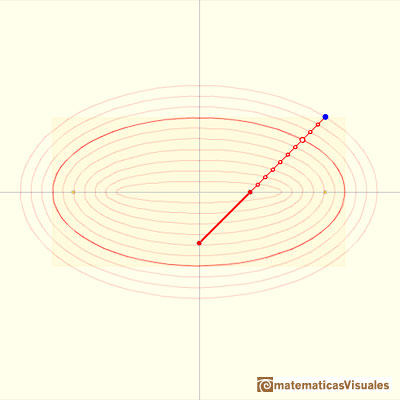
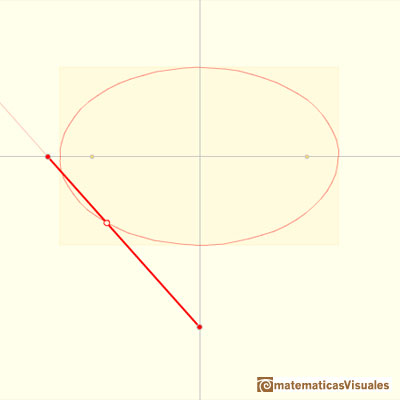
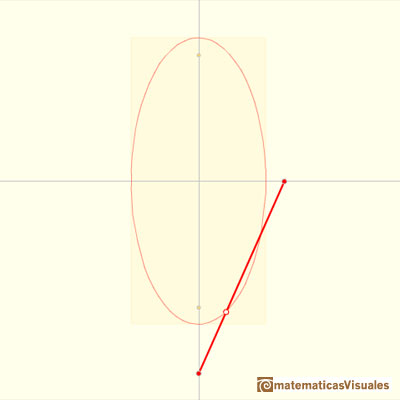
Changing the distances between points we get different ellipses:
This idea was used to build devices for drawing ellipses (called ellipsographs).
This instrument is in the
Museo Nacional de Ciencia y Tecnología in Madrid:
You can get ellipses even if the point P is between the two sliding points:
A circle is a particular case of ellipse:
REFERENCES
Tom Apostol and Mamikon Mnatsakanian, 'New Horizons in Geometry' (Chapter 9. Trammels, ), Mathematical Association of America, 2012.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
Hilbert and Cohn-Vossen, Geometry and the Imagination. Chelsea Publishing Company. pag.278.
Robert C. Yates, 'A Handbook on curves and their properties', J.W.Edwards-Ann Arbor, 1947.
J.L. Coolidge, The Mathematics of great Amateurs. Second Edition. Claredon Press. Oxford. Jan de Witt's proof in page 124.
MORE LINKS
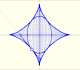
The Astroid is the envelope of a segment of constant length moving with its ends upon two perpendicular lines. It is also the envelope of a family of ellipses, the sum of whose axes is constant.
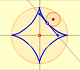
The Astroid is a particular case of a family of curves called hypocycloids.

Every ellipse has two foci and if we add the distance between a point on the ellipse and these two foci we get a constant.

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.
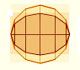
In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.
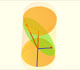
The section of a cylinder by a plane cutting its axis at a single point is an ellipse. A beautiful demonstration uses Dandelin Spheres.

Durer was the first who published in german a method to draw ellipses as cone sections.

Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .

We study different cylinders cut by an oblique plane. The section that we get is an ellipse.

Plane developments of cones cut by an oblique plane. The section is an ellipse.

Plane nets of prisms with a regular base with different side number cut by an oblique plane.
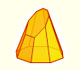
Plane net of pyramids cut by an oblique plane.




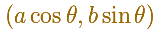
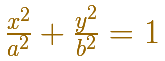


 NEXT
NEXT
 PREVIOUS
PREVIOUS